 por Alvadorn » Dom Mar 06, 2011 13:20
por Alvadorn » Dom Mar 06, 2011 13:20
Eu estou com dificuldade na resolução de duas questões e gostaria de ajuda.
1ª questãoDetermine a equação da reta que passa pelo ponto P e é paralela à reta da equação dada: P(2, -5) e x = 2A solução que eu imaginei, eu não tenho certeza se o racicionio está certo.
solução imaginada escreveu:Sendo x=2, e as retas paralelas a equação também sera x=2.
2ª questão
Eu pensei em fazer algo como:
Porém a resposta correta da equação da reta-suporte é

, não tenho ideia de como chegar nesse resultado.
-
Alvadorn
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Fev 20, 2010 12:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Dom Mar 06, 2011 14:11
por Renato_RJ » Dom Mar 06, 2011 14:11
Boa tarde campeão...
Vamos as definições, se uma reta é paralela a x=2 esta reta pode ser x=3, x =4, etc.. Mas não pode ser x=2, pois seriam a mesma reta !!!
No segundo problema, ele pede a reta da base menor, você descobriu a equação da reta da BASE MAIOR, a base menor é o segmento DC, refaça as contas.... Só uma coisa, eu não entendi o porque da matriz e a coordenada z ter valor igual a 1 (a não ser que você esteja usando um plano paralelo a xy com altura z=1), pois pelo que me consta, um trapézio tem pelo menos dois lados paralelos, logo AB é paralelo a DC, se C tem coordenada (6,5) D terá (x,5) então sua reta seria y = 5...
Abraços e boa sorte nas contas...
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Alvadorn » Dom Mar 06, 2011 14:31
por Alvadorn » Dom Mar 06, 2011 14:31
Renato_RJ escreveu:Boa tarde campeão...
Vamos as definições, se uma reta é paralela a x=2 esta reta pode ser x=3, x =4, etc.. Mas não pode ser x=2, pois seriam a mesma reta !!!
No segundo problema, ele pede a reta da base menor, você descobriu a equação da reta da BASE MAIOR, a base menor é o segmento DC, refaça as contas.... Só uma coisa, eu não entendi o porque da matriz e a coordenada z ter valor igual a 1 (a não ser que você esteja usando um plano paralelo a xy com altura z=1), pois pelo que me consta, um trapézio tem pelo menos dois lados paralelos, logo AB é paralelo a DC, se C tem coordenada (6,5) D terá (x,5) então sua reta seria y = 5...
Abraços e boa sorte nas contas...
Renato.
1ª questãoNa verdade a reta pode ser x =2, até por o enunciado diz isso, e a resposta oferecida pelo autor do livro também da x = 2 como resposta, eu apenas queria entender porque.
2ª questãoO valor de z sendo igual a 1 se deve a
forma segmentaria da equação da reta 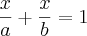
, considerando um ponto generico
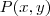
, e fazendo:
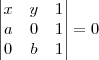
Eu analisei novamente o desenho do gráfico e conclui, sendo D (x,5) como dito por você, e as retas paralelas da base maior com a base menor

, ou seja, por

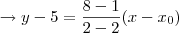
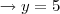
A 2ª questão eu compreendi, mas a 1ª ainda não.
-
Alvadorn
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Fev 20, 2010 12:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Dom Mar 06, 2011 14:46
por Renato_RJ » Dom Mar 06, 2011 14:46
Concorda comigo que se duas retas possuem a mesma equação elas são a mesma reta ?? Teorema da unicidade... Mas se x=2 então a reta é paralela ao eixo Y e com valor constante de x, isto é, qualquer outra reta paralela a ela não poderá assumir o valor de x = 2, então a única reta que poderíamos chamar de paralela a x = 2 e que passe pelos pontos dados, seria ela mesma, o que não faz muito sentido ao menos para mim...
Quanto a matriz, eu nem lembrava da forma segmentária da reta, obrigado por me lembrar dela... Então faz sentido as suas contas, mas você só usou a base errada (acontece, normal)....
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Alvadorn » Dom Mar 06, 2011 15:26
por Alvadorn » Dom Mar 06, 2011 15:26
Renato_RJ escreveu:Concorda comigo que se duas retas possuem a mesma equação elas são a mesma reta ?? Teorema da unicidade... Mas se x=2 então a reta é paralela ao eixo Y e com valor constante de x, isto é, qualquer outra reta paralela a ela não poderá assumir o valor de x = 2, então a única reta que poderíamos chamar de paralela a x = 2 e que passe pelos pontos dados, seria ela mesma, o que não faz muito sentido ao menos para mim...
Quanto a matriz, eu nem lembrava da forma segmentária da reta, obrigado por me lembrar dela... Então faz sentido as suas contas, mas você só usou a base errada (acontece, normal)....
[ ]'s
Renato.
Agora interpretei o que você falou, e fez um pouco de sentido a mim. Duas retas que possuem a mesma equação, não tem de ser necessariamente a mesma reta, pois tem as retas paralelas iguais ou coincidentes. (sendo a e b duas retas,
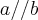
, com
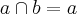
ou

)
Ou isso não confere?
Editado pela última vez por
Alvadorn em Dom Mar 06, 2011 15:50, em um total de 1 vez.
-
Alvadorn
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Fev 20, 2010 12:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Dom Mar 06, 2011 15:33
por Renato_RJ » Dom Mar 06, 2011 15:33
Exatamente, estamos falando a mesma coisa mas em linguagem diferente.... Hehehehehe.... Uma reta passa por exatos dois pontos, se outra reta passa por esses mesmos dois pontos, essas retas são idênticas (a = b)...
[ ]'s
Renato
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2465 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [Estudo da reta] Determinar a equação de uma reta
por Isabelagarcia » Qui Jul 24, 2014 23:45
- 0 Respostas
- 1594 Exibições
- Última mensagem por Isabelagarcia

Qui Jul 24, 2014 23:45
Geometria Analítica
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação da Reta
por aline2010 » Dom Jun 13, 2010 23:16
- 1 Respostas
- 1654 Exibições
- Última mensagem por Elcioschin

Seg Jun 14, 2010 12:16
Geometria Analítica
-
- Equação da reta
por marcio277 » Sex Nov 19, 2010 15:04
- 1 Respostas
- 1526 Exibições
- Última mensagem por Molina

Sex Nov 19, 2010 15:13
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 , não tenho ideia de como chegar nesse resultado.
, não tenho ideia de como chegar nesse resultado.
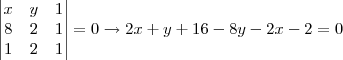
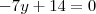



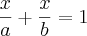 , considerando um ponto generico
, considerando um ponto generico 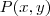 , e fazendo:
, e fazendo: 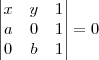
 , ou seja, por
, ou seja, por 
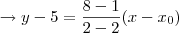
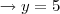
 , com
, com 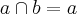 ou
ou  )
) 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.