 por john » Qua Fev 16, 2011 13:01
por john » Qua Fev 16, 2011 13:01

Alguém me pode dizer o domínio desta função?
Ela entra na condição do logaritmo? Não estou entendendo.
Obrigado!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por john » Qua Fev 16, 2011 21:43
por john » Qua Fev 16, 2011 21:43
Ninguém sabe?
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Renato_RJ » Qua Fev 16, 2011 22:07
por Renato_RJ » Qua Fev 16, 2011 22:07
Amigão, tudo em paz ??
Seguinte, eu acho que essa função seja
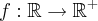
, logo o domínio da função é o conjunto dos Reais..
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por MarceloFantini » Qua Fev 16, 2011 23:22
por MarceloFantini » Qua Fev 16, 2011 23:22
Você decide o domínio. O maior domínio possível é

, mas o domínio sempre deve ser dado. O que você quer dizer com condição do logaritmo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por john » Sex Fev 18, 2011 18:12
por john » Sex Fev 18, 2011 18:12
Por exemplo: ln(x)
O Domínio é {x € IR: x>0}
Aqui não se aplica?
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sex Fev 18, 2011 18:28
por MarceloFantini » Sex Fev 18, 2011 18:28
O maior domínio possível para
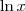
é esse, mas eu reitero:
domínio é arbitrário, respeitando condições de existência. Na função que você postou, não há restrições de condição de existência, logo o
maior domínio possível é

, mas isso não quer dizer que o domínio não possa ser
![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
,
![]e,\pi] ]e,\pi]](/latexrender/pictures/5d7ae4c888b089bf7e94cdf5b4c8e796.png)
, etc.
P.S.: Acho que entendi o que você quer dizer. Você pergunta se pode existir

? Sim, com exceção de

, pois
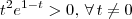
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por john » Sáb Fev 19, 2011 14:31
por john » Sáb Fev 19, 2011 14:31
Então funções desse género é sempre IR?.
Só tenho que ter atenção a ln, a fracções e a raízes certo?
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sáb Fev 19, 2011 16:27
por MarceloFantini » Sáb Fev 19, 2011 16:27
John,
novamente, o domínio é arbitrário. Mas sim, o maior domínio
pode ser o

. E basicamente apenas essas funções, sim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3257 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2891 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1776 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5180 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
-
- Domínio de uma função
por Jonatan » Qui Jul 29, 2010 15:46
- 0 Respostas
- 1870 Exibições
- Última mensagem por Jonatan

Qui Jul 29, 2010 15:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





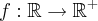 , logo o domínio da função é o conjunto dos Reais..
, logo o domínio da função é o conjunto dos Reais..
 , mas o domínio sempre deve ser dado. O que você quer dizer com condição do logaritmo?
, mas o domínio sempre deve ser dado. O que você quer dizer com condição do logaritmo?


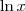 é esse, mas eu reitero: domínio é arbitrário, respeitando condições de existência. Na função que você postou, não há restrições de condição de existência, logo o maior domínio possível é
é esse, mas eu reitero: domínio é arbitrário, respeitando condições de existência. Na função que você postou, não há restrições de condição de existência, logo o maior domínio possível é  , mas isso não quer dizer que o domínio não possa ser
, mas isso não quer dizer que o domínio não possa ser ![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ,
, ![]e,\pi] ]e,\pi]](/latexrender/pictures/5d7ae4c888b089bf7e94cdf5b4c8e796.png) , etc.
, etc. ? Sim, com exceção de
? Sim, com exceção de  , pois
, pois 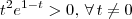 .
.


 . E basicamente apenas essas funções, sim.
. E basicamente apenas essas funções, sim.
