 por john » Seg Fev 14, 2011 20:59
por john » Seg Fev 14, 2011 20:59
Alguém me ajuda a igualar este logaritmo a 0, para obter os zeros da função?
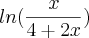
=0
Não faço ideia como resolvê-lo.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Seg Fev 14, 2011 22:09
por Molina » Seg Fev 14, 2011 22:09
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por john » Ter Fev 15, 2011 13:49
por john » Ter Fev 15, 2011 13:49
Obrigado molina.
Agora estava tentando este e não consegui:

=0

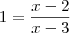

E agora não consigo acabá-lo.
Obrigado pela atenção.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Ter Fev 15, 2011 16:44
por Molina » Ter Fev 15, 2011 16:44
Neste caso, John, não haverá solução, pois jamais o logaritimando será igual a 1, como você pode comprovar fazendo as contas.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por john » Ter Fev 15, 2011 17:45
por john » Ter Fev 15, 2011 17:45
Ok. Então a função não tem zeros, certo?
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Ter Fev 15, 2011 18:07
por Molina » Ter Fev 15, 2011 18:07
john escreveu:Ok. Então a função não tem zeros, certo?
Correto, como pode ser visto
aqui.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por john » Ter Fev 15, 2011 20:30
por john » Ter Fev 15, 2011 20:30
Ok. Obrigado!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1847 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2729 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5265 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2279 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
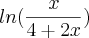 =0
=0

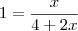




 =0
=0
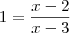







 .
.



