 por Carolziiinhaaah » Sex Fev 04, 2011 15:39
por Carolziiinhaaah » Sex Fev 04, 2011 15:39
Prove que o número
![\sqrt[3]{2 + \frac{10}{9}.\sqrt{3}} + \sqrt[3]{2 - \frac{10}{9}.\sqrt{3}} \sqrt[3]{2 + \frac{10}{9}.\sqrt{3}} + \sqrt[3]{2 - \frac{10}{9}.\sqrt{3}}](/latexrender/pictures/1017250175cb0c7f98831069cf92b056.png)
é inteiro.
gabarito: 2.
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Sex Fev 04, 2011 17:30
por Elcioschin » Sex Fev 04, 2011 17:30
Para facilitar façamos x = 2 + 10*V3/9, y = 2 - 10*V3/9 ----> x + y = 4 ----> xy = 4 - 100*3/81 ----> xy = 8/27 ----> ³V(xy) = 2/3
z = ³Vx + ³Vy ----> Elevando ao cubo:
z³ = (³Vx + ³Vy)³ ----> z³ = x + 3*³V(x²)*³Vy + 3*³Vx*³V(y²) + y ----> z³ = x + y + 3*³Vx*³Vy*(³Vx + ³Vy) ---->
z³ = 4 + 3*³V(xy)*z ----> z³ = 4 + 3*(2/3)*z ----> z³ = 4 + 2z
Esta equação do 3º grau admite uma raiz inteira z = 2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Cleyson007 » Sáb Fev 05, 2011 12:13
por Cleyson007 » Sáb Fev 05, 2011 12:13
Elcio, encontrei que
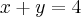
e

, veja:

Resolvendo o sistema,
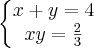
, encontrei:
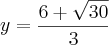
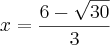
Bom, o exercício pede para provar que o número em questão é inteiro, correto? Ao fazer x + y =
4, já não fica provado que o número de fato é inteiro?
Não consegui entender o que foi feito para demonstrar que admite uma raiz inteira z =
2Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Sáb Fev 05, 2011 13:20
por MarceloFantini » Sáb Fev 05, 2011 13:20
Você está esquecendo o fato de que o número que ele quer na verdade é
![\sqrt[3]{x} + \sqrt[3]{y} \sqrt[3]{x} + \sqrt[3]{y}](/latexrender/pictures/20e2f83c77a482c7a24f102740931df8.png)
, e não

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Sáb Fev 05, 2011 13:56
por Elcioschin » Sáb Fev 05, 2011 13:56
Complementando a resposta do Fantini:
Equação final ----> z³ = 2z + 4 ----> z³ - 2z + 4 = 0
Pesquisa de raízes racionais:
Divisores de 4 ----> + - 1, 2, 4
Divisotes co coeficiente de z³ (1) ----> + - 1
Se houver raízes racionais elas deverão ser dadas pelas relações entre os divisores ----> + - 4/1, 2/1, 1/1
Logo se existirem raízes racinais elas serão INTEIRAS ----> + - 4, 2, 1
Agora basta testar este 6 valores
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Carolziiinhaaah » Sáb Fev 05, 2011 13:59
por Carolziiinhaaah » Sáb Fev 05, 2011 13:59
Obrigada Elcio!

Bastante esclarecedor!
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- poliedro
por Gir » Ter Jan 12, 2010 10:59
- 2 Respostas
- 1667 Exibições
- Última mensagem por Gir

Sex Jan 15, 2010 10:16
Geometria Espacial
-
- Poliedro
por flavio2010 » Seg Jun 28, 2010 23:47
- 1 Respostas
- 23087 Exibições
- Última mensagem por vyhonda

Dom Jul 04, 2010 01:01
Geometria Espacial
-
- Poliedro
por aline2010 » Qui Ago 26, 2010 20:38
- 0 Respostas
- 1160 Exibições
- Última mensagem por aline2010

Qui Ago 26, 2010 20:38
Geometria Espacial
-
- poliedro
por creberson » Ter Set 18, 2012 10:20
- 3 Respostas
- 2740 Exibições
- Última mensagem por Renato_RJ

Ter Set 18, 2012 13:39
Geometria Espacial
-
- Desafio (Poliedro)
por Carolziiinhaaah » Sex Jul 09, 2010 22:22
- 1 Respostas
- 2109 Exibições
- Última mensagem por Tom

Sáb Jul 10, 2010 01:50
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{2 + \frac{10}{9}.\sqrt{3}} + \sqrt[3]{2 - \frac{10}{9}.\sqrt{3}} \sqrt[3]{2 + \frac{10}{9}.\sqrt{3}} + \sqrt[3]{2 - \frac{10}{9}.\sqrt{3}}](/latexrender/pictures/1017250175cb0c7f98831069cf92b056.png) é inteiro.
é inteiro.
![\sqrt[3]{2 + \frac{10}{9}.\sqrt{3}} + \sqrt[3]{2 - \frac{10}{9}.\sqrt{3}} \sqrt[3]{2 + \frac{10}{9}.\sqrt{3}} + \sqrt[3]{2 - \frac{10}{9}.\sqrt{3}}](/latexrender/pictures/1017250175cb0c7f98831069cf92b056.png) é inteiro.
é inteiro.

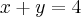 e
e  , veja:
, veja:
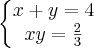 , encontrei:
, encontrei: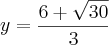
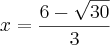

![\sqrt[3]{x} + \sqrt[3]{y} \sqrt[3]{x} + \sqrt[3]{y}](/latexrender/pictures/20e2f83c77a482c7a24f102740931df8.png) , e não
, e não  .
.





 .
.



