 por shark4ever » Dom Jan 30, 2011 13:59
por shark4ever » Dom Jan 30, 2011 13:59
Saudações a todos,
Tenho desde ja uma duvida a qual agradeço desde ja a vossa ajuda.
Tenho a seguinte função

e pretendia obter o valor de K, nao sei se me estou a fazer entender.
cumpr
Editado pela última vez por
shark4ever em Dom Jan 30, 2011 21:10, em um total de 1 vez.
-
shark4ever
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jan 30, 2011 13:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Jan 30, 2011 20:15
por Molina » Dom Jan 30, 2011 20:15
Boa noite, amigo.
Não ficou muito claro a exibição da integral.
Em cima uma aparece embaixo da outra.
Já na de baixo você as colocou como numa soma.
Tem como deixar mais claro como ela estão?
Abraços!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por shark4ever » Dom Jan 30, 2011 21:15
por shark4ever » Dom Jan 30, 2011 21:15
Não sei se agora ja esta mais claro.
Nao se sei o passo seguinte sera assim:
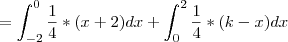
-
shark4ever
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jan 30, 2011 13:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Seg Jan 31, 2011 10:12
por Elcioschin » Seg Jan 31, 2011 10:12
Ainda não ficou claro
Tem-se uma função f(x) e quer-se descobrir o valor de K
Para isto deve ser dito qual é o valor de f(x), senão o problema é impossível
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por shark4ever » Seg Jan 31, 2011 13:35
por shark4ever » Seg Jan 31, 2011 13:35
-
shark4ever
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jan 30, 2011 13:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qui Fev 03, 2011 08:48
por LuizAquino » Qui Fev 03, 2011 08:48
O enunciado do exercício diz o seguinte:
Considere a variável aleatória X com a seguinte função de probabilidade:
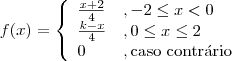
a) Determine, justificando detalhadamente, o valor da constante k.
Para que uma função seja uma
função de probabilidade ela deve ser sempre positiva e a integral em todo os seu domínio deve ser igual a 1.
O domínio dessa função é todo o conjunto dos números reais, então devemos ter:

Note que essa função está definida em intervalos, de modo que fora do intervalo [-2, 2] ela é zero. Portanto, podemos simplificar essa integral para:

Por fim, a função tem uma expressão diferente para os intervalos [-2, 0) e [0, 2]. Portanto, temos que:

Note que esse limite que apareceu na primeira integral é só para dar conta do fato que em x=0 a função está definida como (k-x)/4 e não como (x+2)/4.
Resolvendo as integrais, obtemos:
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1](/latexrender/pictures/fe768a2ceb74b7a61b6b54c44f1af23d.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1](/latexrender/pictures/eddb21f7336363a3c1dec89adaadd9ac.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1](/latexrender/pictures/9719681947903a61d9d411e92f789825.png)


Sendo assim, para k=2 a integral em todo domínio de f será igual a 1. Além disso, note que para k=2 a função é sempre positiva.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 3934 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4390 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4117 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2681 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2696 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





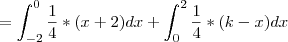






![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{x^2}{2} +2x\right]_{-2}^b + \frac{1}{4}\left[kx - \frac{x^2}{2}\right]_0^2 = 1](/latexrender/pictures/fe768a2ceb74b7a61b6b54c44f1af23d.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} +2b - \left(\frac{(-2)^2}{2} +2(-2)\right)\right] + \frac{1}{4}\left[2k - \frac{2^2}{2} - \left(0\cdot k - \frac{0^2}{2}\right) \right] = 1](/latexrender/pictures/eddb21f7336363a3c1dec89adaadd9ac.png)
![\lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1 \lim_{b\to 0^-} \frac{1}{4}\left[\frac{b^2}{2} + 2b + 2\right] + \frac{1}{4}(2k - 2) = 1](/latexrender/pictures/9719681947903a61d9d411e92f789825.png)








