Verifique se A ou B é subgrupo do grupo multiplicativo
 :
:
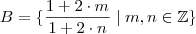
Eu acho que somente A é subgrupo, mas gostaria da opinião de vocês, estou certo ?
Abraços,
Renato.

 :
:
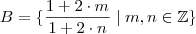


 ???
??? 
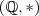 , onde * é a operação de multiplicação. Atenção: Não confundir isso com o conjunto
, onde * é a operação de multiplicação. Atenção: Não confundir isso com o conjunto  .
.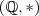 , precisamos mostrar que A e B são subconjuntos de
, precisamos mostrar que A e B são subconjuntos de  e além disso que
e além disso que 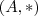 e
e  são grupos. Nesse exercício em particular tanto A e B são subgrupos, pois atendem a essas condições.
são grupos. Nesse exercício em particular tanto A e B são subgrupos, pois atendem a essas condições.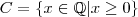 não é subgrupo de
não é subgrupo de 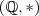 , apesar de C ser um subconjunto de
, apesar de C ser um subconjunto de  . Isso porque nesse caso
. Isso porque nesse caso 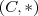 não é grupo, pois há um elemento no conjunto que não possui o simétrico da operação dada (note que não há inverso multiplicativo de 0).
não é grupo, pois há um elemento no conjunto que não possui o simétrico da operação dada (note que não há inverso multiplicativo de 0).



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.