 por ARCS » Qua Jan 05, 2011 21:23
por ARCS » Qua Jan 05, 2011 21:23
Como calcular o seguinte limite usando os teoremas
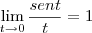
e

.
Por favor explique o passo a passo da resolução.

-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por OtavioBonassi » Qua Jan 05, 2011 21:32
por OtavioBonassi » Qua Jan 05, 2011 21:32
Cara, pelo que eu vi ,utilizando só esses teoremas ai o que voce pode fazer é destrinchar os dois termos , por exempo a parte do sen à quinta ... voce deixa sen² . sen² . sen , ai esses sen² voce substitui por (1 - cos²) , e a parte debaixo voce destrincha também e tenta encaixar igual aos teoremas, creio que dê certo desse jeito que te falei
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teoremas e corolários para séries
por Aprendiz2012 » Qua Out 03, 2012 10:51
- 1 Respostas
- 1472 Exibições
- Última mensagem por young_jedi

Qua Out 03, 2012 11:04
Sequências
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4432 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
-
- [Demostrações]Demostrações de alguns teoremas e proposições
por DIego Gomes » Seg Dez 16, 2013 23:05
- 4 Respostas
- 2212 Exibições
- Última mensagem por DIego Gomes

Seg Dez 16, 2013 23:42
Álgebra Elementar
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1616 Exibições
- Última mensagem por DanielFerreira

Sex Abr 17, 2015 20:32
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
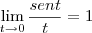 e
e  .
.

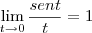 e
e  .
.

