 por iveli » Sáb Dez 11, 2010 22:47
por iveli » Sáb Dez 11, 2010 22:47
"(UNICAMP) Determinar as equações cartesianas dos círculos que passam pelos pontos (2a;0) e (0;2b), centrados, respectivamente, em (a;0) e (0;b), em que a e b são números positivos. Determine os pontos de intersecção desses círculos."
Eu consegui encontrar os raios (raio1=a e raio 2=b) e as equações das circunferências:


Nessa parte, eu igualo as equações mas não consigo terminar os cálculos.
A resposta do exercício é: "Os pontos de intersecção são (0;0) e
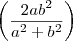
;

"
Muito obrigada pela ajuda!
-
iveli
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Dez 11, 2010 21:58
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Geomática
- Andamento: formado
 por meuemail » Dom Dez 12, 2010 04:54
por meuemail » Dom Dez 12, 2010 04:54
É a primeira vez que escrevo aqui, não sei se a resposta vai esta mal formatada ou sem formalidade matemática,
qualquer coisa é só me avisar por e-mail, o meu é [meuemail2@ymail.com].
Mandei anexo no word colorido.
Dei uma desenferrujada boa com estas continhas, rsrsrsrrs. Até mais.
- Anexos
-
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
-
meuemail
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Dez 11, 2010 23:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por iveli » Qua Dez 15, 2010 18:23
por iveli » Qua Dez 15, 2010 18:23
Agora entendi onde eu estava errando. Muito obrigada, você realmente me ajudou!

-
iveli
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Dez 11, 2010 21:58
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Geomática
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- QUESTÃO DE GEOMETRIA ANALÍTICA (DUVIDA!!!)
por hudeslan » Qui Ago 13, 2009 18:15
- 1 Respostas
- 1816 Exibições
- Última mensagem por Felipe Schucman

Qui Ago 13, 2009 19:24
Geometria Analítica
-
- Geometria Analitica - Circunferência - Duvida
por PiterPaulo » Sáb Mai 11, 2013 21:12
- 0 Respostas
- 1441 Exibições
- Última mensagem por PiterPaulo

Sáb Mai 11, 2013 21:12
Geometria Analítica
-
- Geometria Analítica [Dúvida] sobre cônicas
por pablohas » Sáb Dez 04, 2010 12:55
- 6 Respostas
- 5720 Exibições
- Última mensagem por pablohas

Seg Dez 06, 2010 20:17
Geometria Analítica
-
- [Algebra linear e geometria analitica] Duvida
por lucasdemirand » Sáb Jul 06, 2013 15:32
- 1 Respostas
- 1406 Exibições
- Última mensagem por e8group

Dom Jul 07, 2013 21:27
Álgebra Linear
-
- Circulos Tangentes a Duas Retas
por nakagumahissao » Qua Abr 04, 2012 20:13
- 2 Respostas
- 3507 Exibições
- Última mensagem por nakagumahissao

Ter Mai 01, 2012 16:40
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ;
; "
"


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.