 por nayane » Qua Nov 24, 2010 20:48
por nayane » Qua Nov 24, 2010 20:48
Uma das raízes do polinômio x³ + 2x² - 7x - 2 é 2. Qual o produto das outras raizes?
Nayane
-

nayane
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sex Set 10, 2010 10:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em ciências biológicas
- Andamento: cursando
 por Molina » Qua Nov 24, 2010 22:03
por Molina » Qua Nov 24, 2010 22:03
Boa noite, Nayane.
Para descobrir as outras raízes você pode fazer a fatorização deste polinômio, reduzindo seu grau. O melhor modo de fazer isso é dividindo este polinômio por x - 2, já que sabemos que 2 é uma das raízes.
Fazendo a divisão de um polinômio de grau 3 por um polinômio de grau 1 você encontrará um polinômio de grau 2. Usando a fórmula de Báskara você encontrar as raízes. Então basta multiplicá-las.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por nayane » Qui Nov 25, 2010 10:08
por nayane » Qui Nov 25, 2010 10:08
Molina agradeço a explicação, mas confesso que fiquei com uma duvida, não sabendo se fiz exatamente o que me dissestes.
Eu fiz o seguinte: na divisão do termo x³+2x²-7x-2 por x-2 o resultado foi x² - 7 com resto 12.
Agora estou confusa e não sei o que fazer, vc poderia me ajudar?

Diante mão agradeço.
Nayane
-

nayane
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sex Set 10, 2010 10:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em ciências biológicas
- Andamento: cursando
 por Molina » Qui Nov 25, 2010 16:55
por Molina » Qui Nov 25, 2010 16:55
nayane escreveu:Molina agradeço a explicação, mas confesso que fiquei com uma duvida, não sabendo se fiz exatamente o que me dissestes.
Eu fiz o seguinte: na divisão do termo x³+2x²-7x-2 por x-2 o resultado foi x² - 7 com resto 12.
Agora estou confusa e não sei o que fazer, vc poderia me ajudar?

Diante mão agradeço.
Boa tarde, Nayane.
Na verdade a divisão de
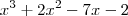
por

é

. Você pode obter este valor através do
método das chaves (Euclidiano) ou até mesmo usando o
método de Briot Ruffini.
De qualquer forma agora basta encontrar as raízes de
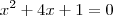
.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por nayane » Qui Nov 25, 2010 21:03
por nayane » Qui Nov 25, 2010 21:03
Molina obrigada, realmente não soube resolvi a divisão, obrigada também pelo site foi muito importante
Nayane
-

nayane
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sex Set 10, 2010 10:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em ciências biológicas
- Andamento: cursando
Voltar para Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








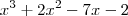 por
por  é
é  . Você pode obter este valor através do método das chaves (Euclidiano) ou até mesmo usando o método de Briot Ruffini.
. Você pode obter este valor através do método das chaves (Euclidiano) ou até mesmo usando o método de Briot Ruffini.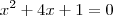 .
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.