 por lucasla » Qui Nov 11, 2010 17:44
por lucasla » Qui Nov 11, 2010 17:44
Estou com uma dúvida em uma questão simples de Arranjos, até já resolvi a questão, mas uma dúvida ficou:
A questão é a seguinte: Tenho um conjunto de 9 números {1, 2, 3, 4, 5, 6, 7, 8, 9}, e quero saber quantos grupos de 7 elementos distintos posso formar com esses números, de modo que os números 5 e 6 fiquem sempre juntos e nessa mesma ordem.
Eu resolvi a questão da seguinte maneira:
Imaginando 7 espaços, os 2 primeiros espaços são reservados para o 5 e o 6, e os outros espaços vão ser arranjos de 7 elementos 5 a 5. E como o 5 e o 6 podem mudar de posição 6 vezes, multiplico esse arranjo por 6. Ou seja A7,5 * 6 = 15120 elementos diferentes. (que é a resposta correta)
_1_ x _1_ x _7_ x _6 x _5_ x _4_ x _3_ (*6) = 15120
blz, mas fazendo da seguinte maneira, que eu imaginava que também devia dar certo, não obtenho o mesmo resultado:
Como o 5 e o 6 ficarão sempre juntos e nessa ordem, posso imaginá-los como sendo um único elemento que gasta apenas 1 espaço (posso mesmo?), logo teria 8 elementos {1, 2, 3, 4, 5-6, 7, 8, 9} e 6 espaços, bastando fazer o arranjo de 8 elementos 6 a 6. Mas isso me retorna 20160.
Por que fazer isso está errado?
-
lucasla
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 11, 2010 17:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: num interessa
- Andamento: cursando
 por MarceloFantini » Qui Nov 11, 2010 18:20
por MarceloFantini » Qui Nov 11, 2010 18:20
Se os números 5 e 6 devem estar juntos, podemos considerá-los como um único bloco. E como também não trocam de ordem, só existe uma única maneira de posicioná-los. Logo, sobre 7 elementos distintos. Assim, o número de possibilidades será
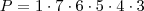
. Porém, não necessariamente os números 5 e 6 devem estar posicionados no começo. Podem ser colocados no meio, ou no final, ou depois. Enfim, a lógica é que ele pode trocar de ordem, e para representar essa troca de ordem multiplicamos por 6, que é o número de posições que ele pode ocupar:
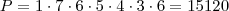
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lucasla » Sex Nov 12, 2010 02:40
por lucasla » Sex Nov 12, 2010 02:40
certo, foi assim que resolvi, mas por que que daquela segunda forma que eu tentei não funciona também?
-
lucasla
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 11, 2010 17:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: num interessa
- Andamento: cursando
 por MarceloFantini » Sex Nov 12, 2010 15:19
por MarceloFantini » Sex Nov 12, 2010 15:19
Eu não me lembro a forma de arranjo, mas você tem 7 espaços para preencher e 2 já estão ocupados, portanto acredito que você também tenha que descontar essa quantidade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em combinatória
 por renataf » Seg Dez 06, 2010 16:25
por renataf » Seg Dez 06, 2010 16:25
- 3 Respostas
- 8040 Exibições
- Última mensagem por renataf

Seg Dez 06, 2010 21:24
Estatística
-
- Dúvida em Combinatória - Competição
por andymath » Sex Mai 21, 2010 23:04
- 1 Respostas
- 1502 Exibições
- Última mensagem por angeruzzi

Ter Jun 08, 2010 02:55
Estatística
-
- [ANALISE COMBINATORIA]duvida
por Fabricio dalla » Seg Set 19, 2011 15:24
- 1 Respostas
- 7861 Exibições
- Última mensagem por Neperiano

Seg Set 19, 2011 18:04
Estatística
-
- [Análise combinatória] dúvida
por Tiego » Qua Mai 09, 2012 10:32
- 2 Respostas
- 2811 Exibições
- Última mensagem por joaofonseca

Qui Mai 17, 2012 08:32
Estatística
-
- [Análise combinatória] dúvida
por Tiego » Qua Mai 09, 2012 10:33
- 1 Respostas
- 2056 Exibições
- Última mensagem por fraol

Ter Mai 15, 2012 22:55
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


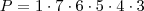 . Porém, não necessariamente os números 5 e 6 devem estar posicionados no começo. Podem ser colocados no meio, ou no final, ou depois. Enfim, a lógica é que ele pode trocar de ordem, e para representar essa troca de ordem multiplicamos por 6, que é o número de posições que ele pode ocupar:
. Porém, não necessariamente os números 5 e 6 devem estar posicionados no começo. Podem ser colocados no meio, ou no final, ou depois. Enfim, a lógica é que ele pode trocar de ordem, e para representar essa troca de ordem multiplicamos por 6, que é o número de posições que ele pode ocupar: 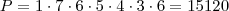 .
.






