 por Marcelo C Delgado » Seg Nov 08, 2010 16:01
por Marcelo C Delgado » Seg Nov 08, 2010 16:01
Boa tarde pessoal,
Estou com uma dúvida no problema abaixo.
- Num triângulo dois catetos adjacentes "a" e "b" são respectivamente 30 e 40mm, e o ângulo oposto ao cateto "b" vale 60°. Qual o valor do ângulo oposto ao cateto "a"?
Um abraço a todos.
Marcelo C. Delgado
-
Marcelo C Delgado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Set 10, 2010 18:08
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico Mecânico
- Andamento: cursando
 por andrefahl » Seg Nov 08, 2010 17:36
por andrefahl » Seg Nov 08, 2010 17:36
Olá Marcelo,
Olha vc pode resolver usando a lei dos senos:
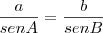
onde a e b são os lados respctivamente opostos ao ângulos A e B.
No caso do problem, ele quer saber o angulo oposto ao lado a e vc tem todos os outros dados.
Daí fica:

tenta resolve desse jeito e ve se ajuda...
acho q deve da certo =)
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por Marcelo C Delgado » Ter Nov 09, 2010 22:27
por Marcelo C Delgado » Ter Nov 09, 2010 22:27
André,
Valeu pela ajuda.
A solução é realmente pela lei dos senos.
A resposta para esse problema é 40°30'19"
Um forte abraço.
Marcelo C. Delgado
-
Marcelo C Delgado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Set 10, 2010 18:08
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico Mecânico
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Triangulo
por ginrj » Ter Abr 28, 2009 20:58
- 3 Respostas
- 3786 Exibições
- Última mensagem por ginrj

Sáb Mai 02, 2009 12:30
Geometria Plana
-
- Triângulo.
por Molina » Qua Mai 13, 2009 23:20
- 2 Respostas
- 2148 Exibições
- Última mensagem por Molina

Qui Mai 14, 2009 19:04
Geometria Plana
-
- Triângulo
por cristina » Seg Set 14, 2009 18:49
- 5 Respostas
- 3024 Exibições
- Última mensagem por Marcampucio

Ter Set 15, 2009 16:44
Trigonometria
-
- Triângulo
por Fogodc » Seg Abr 05, 2010 23:39
- 1 Respostas
- 1939 Exibições
- Última mensagem por Fogodc

Qua Abr 07, 2010 11:37
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


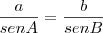


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
