Estou estudando matrizes e determinantes... e estou com duas questões que estou com dúvidas ( quanto à 1ª, gostaria de saber se está correto o modo que a resolvi!!!, quanto à 2ª, não estou conseguindo resolver e gostaria que me ajudasse.)
As questões são essas --> 01) (FGV) Considere a equação matricial
 , onde
, onde 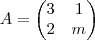 ;
; 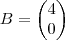 ;
; 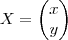
a) Para que valores de
 a equação tem solução única?
a equação tem solução única?b) Resolva a equação para
 .
.Resolvi da seguinte maneira ---> a)
 .
. 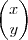 =
=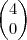 .
.Resolvendo a multiplicação das matrizes, encontrei as duas equações:
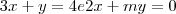 .
.Calculei o determinante dessas duas equações (que formam um sistema), observando que o problema diz que o valor de
 tem que fazer com que a equação possua solução única (SPD-Sistema Possível e Determinado), ou seja
tem que fazer com que a equação possua solução única (SPD-Sistema Possível e Determinado), ou seja  tem que ser diferente de 0.
tem que ser diferente de 0.Encontrei como resultado
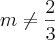 .
.02) (FGV) A matriz
 é inversa da matriz
é inversa da matriz .
.
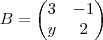 .
.Nessas condições, podemos afirmar que a soma
 vale:
vale: a) -1 b) -2 c) -3 d) -4 e) -5
*Acredito eu que a questão está dizendo que
 , mas, não consegui resolvê-la por aí de maneira alguma!!!
, mas, não consegui resolvê-la por aí de maneira alguma!!!Gostaria que me ajudasse!!!
Até mais.


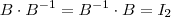
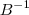 é única e
é única e  , segue que:
, segue que:

 e
e  . Você deverá obter a alternativa (c) para a soma procurada.
. Você deverá obter a alternativa (c) para a soma procurada.
 .
.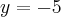 .
.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.