Achei o problema interessante (IME 1971?) e vi duas respostas possíveis no google:
Tem dois raciocínios possíveis que chegam na resposta, coincidentemente é a alternativa com o maior número tambem:
Método 1: pegue um lugar e um grupo de 5 pessoas, de quantas maneiras podemos preencher um lugar tendo 5 escolhas possíveis? 5. Mas são dois lugares por degrau e dois grupos de 5 escolhas, então 5 * 5. E ainda duas formas de preencher os dois lugares, AB ou BA, então 5 * 5 * 2. Repita para mais um degrau, mas reduza o grupo de pessoas disponíveis para a escolha, pois uma escolha já foi feita, fica 4 * 4 * 2. No quinto degrau restará uma moça e um rapaz, 1 * 1 * 2. A expressão completa fica
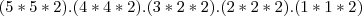
. Que pode ser escrita tambem como
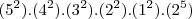
.
Método 2: imagine 5 cadeiras e 5 pessoas, de quantas maneiras podemos preencher as 5 cadeiras com 5 pessoas? Fatorial de 5. Agora dobre o problema, um grupo de 5 pessoas para uma fileira e outro grupo de 5 pessoas para outra fileira. Individualmente são dois 5!. O problema agora é visualizar duas fileiras de 5 cadeiras cada emparelhadas. Uma analogia que pode ser feita é assim, imagina cinco interruptores lado a lado, cada interruptor pode estar ligado ou desligado, assim como cada casal pode ser AB ou BA. Quantas combinações de ligado/desligado podem ser feitas com 5 interruptores lado a lado? Dá um total de 32. No final fica 5! * 5! * 32.
Fundamentalmente os dois métodos são iguais, mas o primeiro é mais manual e o segundo "agrupa" o problema em blocos.
É parecido com uma questão da
Fuvest 2008. A diferença é que na questão da fuvest puseram duas condicionais pra complicar um pouco mais

(mas repara que o enunciado já facilita um pouco ao ordenar os casos já do mais específico para o menos específico, se vc tentar resolver numa ordem diferente da que já foi dada, se enrola todo)


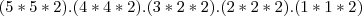 . Que pode ser escrita tambem como
. Que pode ser escrita tambem como 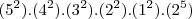 .
. (mas repara que o enunciado já facilita um pouco ao ordenar os casos já do mais específico para o menos específico, se vc tentar resolver numa ordem diferente da que já foi dada, se enrola todo)
(mas repara que o enunciado já facilita um pouco ao ordenar os casos já do mais específico para o menos específico, se vc tentar resolver numa ordem diferente da que já foi dada, se enrola todo)

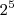 .
.
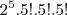
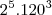
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.