Seção para postagens de problemas matemáticos do cotidiano, reportagens, casos interessantes, polêmicos ou curiosos.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Layna Cardoso » Ter Mar 16, 2010 20:49
por Layna Cardoso » Ter Mar 16, 2010 20:49
Bom , embora essa duvida possa ser um pouco idiota .. eu preciso de ajuda !
ér
1234³
2468³
já tentei de várias fomas : cancelamento , resolver a potenciação primeiro , cortar o ³'
aff' , desculpe gente , mas nao tô conseguindo .!
Por Favor , me ajude

-
Layna Cardoso
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 16, 2010 20:30
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Ter Mar 16, 2010 21:37
por Molina » Ter Mar 16, 2010 21:37
Layna Cardoso escreveu:Bom , embora essa duvida possa ser um pouco idiota .. eu preciso de ajuda !
ér
1234³
2468³
já tentei de várias fomas : cancelamento , resolver a potenciação primeiro , cortar o ³'
aff' , desculpe gente , mas nao tô conseguindo .!
Por Favor , me ajude

Boa noite, Layna.
O que você quer descobrir é isso:
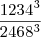
Certo?
O que vamos fazer é fatorar este número de baixo (sem os expoentes). Note que ele (sem o expoente) é o dobro do de cima. Então podemos escrevê-lo assim:
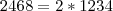
. Logo:
 Agora podemos simplificar...
Agora podemos simplificar...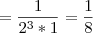
Qualquer dúvida informe.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Problemas do Cotidiano
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PRECISO DE AJUDA!
por Lurdes » Sex Jul 09, 2010 23:22
- 1 Respostas
- 3417 Exibições
- Última mensagem por Neperiano

Qui Set 29, 2011 16:45
Problemas do Cotidiano
-
- preciso de ajuda...
por apoliveirarj » Qua Jul 21, 2010 12:25
- 5 Respostas
- 4164 Exibições
- Última mensagem por apoliveirarj

Qui Jul 22, 2010 12:52
Sistemas de Equações
-
- preciso de ajuda...
por apoliveirarj » Sáb Jul 24, 2010 19:10
- 1 Respostas
- 3045 Exibições
- Última mensagem por Neperiano

Sex Set 17, 2010 15:00
Estatística
-
- preciso de ajuda:
por angeloka » Ter Out 05, 2010 23:00
- 1 Respostas
- 2143 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 23:39
Álgebra Elementar
-
- preciso de ajuda
por arima » Qui Nov 25, 2010 12:30
- 2 Respostas
- 2035 Exibições
- Última mensagem por arima

Qui Nov 25, 2010 13:47
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


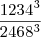
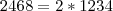 . Logo:
. Logo:
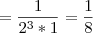


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
