Seção para postagens de problemas matemáticos do cotidiano, reportagens, casos interessantes, polêmicos ou curiosos.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por bia rosendo » Seg Fev 28, 2011 22:59
por bia rosendo » Seg Fev 28, 2011 22:59
Na oficina de trabalhos manuais, uma equipe de detentos realizou 2/5 de um trabalho em 8 dias, trabalhando 6 horas por dia. Mantendo a mesma produtividade por hora e trabalhando 2 horas a mais por dia, essa mesma equipe terminará o projeto em mais:
a)8 dias
b)9 dias
c)10 dias
d)11 dias
e)12 dias
-
bia rosendo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Fev 22, 2011 22:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por gichan » Ter Mar 01, 2011 09:55
por gichan » Ter Mar 01, 2011 09:55
A equipe realizou 2/5 de um trabalho T em 8 dias trabalhando 6 horas em cada um (num total parcial de 48h), então temos:
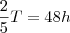
, isolando o lado da hora:
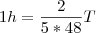
---> Essa é a produtividade. Eles realizam
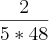
de Trabalho em 1hora.
Porém, agora, a realização do serviço será de 8h por dia e ainda há 3/5 de trabalho a continuar.
Portanto, multiplicando o número de dias "x" pelo de horas, que são 8, teremos o número de horas total para realizar o restante do trabalho. E ainda, multiplicando o número total de horas pela produtividade (o quanto de trabalho eles fazem em 1hora), encontraremos qntos dias eles demoram para realizar o resto do trabalho, nesta equação:

Só desenvolver a equação agora.

Qualquer dúvida na explicação ou no problema, continue perguntando! =]
-

gichan
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Jul 19, 2010 15:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: formado
Voltar para Problemas do Cotidiano
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12986 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10965 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15109 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5023 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4791 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


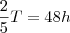 , isolando o lado da hora:
, isolando o lado da hora: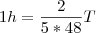 ---> Essa é a produtividade. Eles realizam
---> Essa é a produtividade. Eles realizam 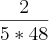 de Trabalho em 1hora.
de Trabalho em 1hora.







