olá... tenho feitos algumas provas do CESPE e percebí que cai muito questões assim e não sei raciocinar em cima delas:
a soma de 3 números inteiros positivos é igual ao maior número inteiro de 5 algrismos distintos. Se adicionarmos a cada um dos números o maior número inteiro de 3 algarismos, a nova soma será igual a :
a) 102996
b) 102960
c) 102876
d) 101726
e) 101762
E agora?????
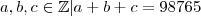, de acordo?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)