Sub-seção para materiais das disciplinas relacionadas ao cálculo.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por sandra silva » Dom Set 14, 2008 20:29
por sandra silva » Dom Set 14, 2008 20:29
tenho esta duvida
(raix quadrada de 4x^2+ 3x + 7)- x (-x fora da raiz )
Lim quando xtende a + infinito
o conjugado ; (?4x2+ 3x+7 -x) (?4x2+ 3x+7 +x) / (?4x2+ 3x+7 +x=
4x+3x+7- x/?4x2+ 3x+7+x =6x+7/?4x2+ 3x+7 +x =6/5
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
 por juliomarcos » Seg Set 15, 2008 19:16
por juliomarcos » Seg Set 15, 2008 19:16
Sandra, tenta escrever sua dúvida usando o LaTeX. É melhor pra a gente entender.
-
juliomarcos
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Set 14, 2008 00:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por sandra silva » Ter Set 16, 2008 00:44
por sandra silva » Ter Set 16, 2008 00:44
sqrt{4x^2+3x +7}-x
lim_{+infinito}
usei o conjugado e gostaria de saber onde errei, conforme informação anterior
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
 por Molina » Ter Set 16, 2008 01:03
por Molina » Ter Set 16, 2008 01:03
sandra silva escreveu:sqrt{4x^2+3x +7}-x
lim_{+infinito}
usei o conjugado e gostaria de saber onde errei, conforme informação anterior
coloque
![[tex] [tex]](/latexrender/pictures/ffdc30d5c40062d678765bdcd9e907d2.png)
antes do codigo em LaTeX e o mesmo código com uma / (barra) antes do tex no final.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por sandra silva » Ter Set 16, 2008 20:29
por sandra silva » Ter Set 16, 2008 20:29
Colega, naoa sei usar o latex pois nao encontrei o infinito por isso escrevi
segue a questao
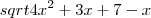
\lim_+infinito
conforme os calculos que envie acima por favor veja onde errei
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
 por sandra silva » Ter Set 16, 2008 20:30
por sandra silva » Ter Set 16, 2008 20:30
usei o conjugado
obrigada
sandra
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
 por sandra silva » Ter Set 16, 2008 21:02
por sandra silva » Ter Set 16, 2008 21:02
\sqrt[{4x^2+3x +7}-x
\lim_{\infty}
fix o conjugado, mas nao sei se esta certo
-
sandra silva
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Ago 26, 2008 22:00
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: lic em matematica
- Andamento: cursando
 por admin » Ter Set 23, 2008 16:28
por admin » Ter Set 23, 2008 16:28
Olá Sandra!
Se entendi a expressão, você pretendia escrever:
![\lim_{x \rightarrow +\infty} \left[ \sqrt{4x^2+3x+7}-x \right] = ? \lim_{x \rightarrow +\infty} \left[ \sqrt{4x^2+3x+7}-x \right] = ?](/latexrender/pictures/5ae8b52245c36a06c0137f2071dc6342.png)
Onde temos uma indeterminação do tipo

.
Podemos sim multiplicar pelo conjugado o numerador e demoninador, pois a expressão não é alterada (é o mesmo que multiplicar por 1). Mas, depois teremos que fazer um passo que já pode ser feito agora. Tente colocar

em evidência:
![L = \lim_{x \rightarrow +\infty} \left( \sqrt{4x^2+3x+7}-x \right) =
\lim_{x \rightarrow +\infty} \left[ x \left(\frac{\sqrt{4x^2+3x+7}}{x}-1 \right) \right] L = \lim_{x \rightarrow +\infty} \left( \sqrt{4x^2+3x+7}-x \right) =
\lim_{x \rightarrow +\infty} \left[ x \left(\frac{\sqrt{4x^2+3x+7}}{x}-1 \right) \right]](/latexrender/pictures/411210032b8b04c396c18c956c99cd00.png)
Depois:
![L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{\frac{4x^2+3x+7}{x^2}}-1 \right) \right] L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{\frac{4x^2+3x+7}{x^2}}-1 \right) \right]](/latexrender/pictures/942af66a0b07d3c156da0d2dd68e4eb3.png)
![L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{4+\frac{3}{x}+\frac{7}{x^2}}-1 \right) \right] L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{4+\frac{3}{x}+\frac{7}{x^2}}-1 \right) \right]](/latexrender/pictures/8ee1c1e07977439109c51fdc27a3812e.png)
No limite teremos:
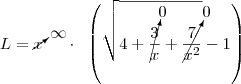
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6480 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4518 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2646 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5547 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





![[tex] [tex]](/latexrender/pictures/ffdc30d5c40062d678765bdcd9e907d2.png) antes do codigo em LaTeX e o mesmo código com uma / (barra) antes do tex no final.
antes do codigo em LaTeX e o mesmo código com uma / (barra) antes do tex no final.
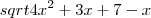



![\lim_{x \rightarrow +\infty} \left[ \sqrt{4x^2+3x+7}-x \right] = ? \lim_{x \rightarrow +\infty} \left[ \sqrt{4x^2+3x+7}-x \right] = ?](/latexrender/pictures/5ae8b52245c36a06c0137f2071dc6342.png)
 .
. em evidência:
em evidência:![L = \lim_{x \rightarrow +\infty} \left( \sqrt{4x^2+3x+7}-x \right) =
\lim_{x \rightarrow +\infty} \left[ x \left(\frac{\sqrt{4x^2+3x+7}}{x}-1 \right) \right] L = \lim_{x \rightarrow +\infty} \left( \sqrt{4x^2+3x+7}-x \right) =
\lim_{x \rightarrow +\infty} \left[ x \left(\frac{\sqrt{4x^2+3x+7}}{x}-1 \right) \right]](/latexrender/pictures/411210032b8b04c396c18c956c99cd00.png)
![L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{\frac{4x^2+3x+7}{x^2}}-1 \right) \right] L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{\frac{4x^2+3x+7}{x^2}}-1 \right) \right]](/latexrender/pictures/942af66a0b07d3c156da0d2dd68e4eb3.png)
![L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{4+\frac{3}{x}+\frac{7}{x^2}}-1 \right) \right] L = \lim_{x \rightarrow +\infty} \left[ x \left(\sqrt{4+\frac{3}{x}+\frac{7}{x^2}}-1 \right) \right]](/latexrender/pictures/8ee1c1e07977439109c51fdc27a3812e.png)
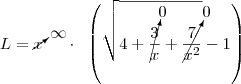

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.