Localizado num ponto A, ao lado de seu cão e na margem de um rio de 10 metros de largura, o pesquisador lança um disco na margem oposta desse rio, num ponto B, localizado a uma distância de 100 metros do ponto A (medida paralelamente à margem do rio). O cão então segue em busca do disco, percorrendo uma parte do trajeto por terra e a uma valocidade
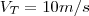 e mergulhando no rio num ponto C, percorrendo outra parte do trajeto na água com velocidade
e mergulhando no rio num ponto C, percorrendo outra parte do trajeto na água com velocidade 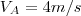 . Medindo a distância entre A e C, ele encontrou 96m.
. Medindo a distância entre A e C, ele encontrou 96m. Mais tarde, calculando a que distância do ponto A o cão deveria pular na água afim de que o tempo para chegar até o disco fosse minimizado, o pesquisador encontrou um resultado surpriendente:
Fazendo um esboço do problema, temos:

onde a linha em vermelho foi o trajeto percorrido pelo cão.
O tempo gasto em terra é:
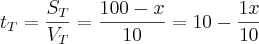
O tempo gasto na água é:
![{t}_{A}=\frac{{S}_{A}}{{V}_{A}}=\frac{\sqrt[]{100+{x}^{2}}}{4} {t}_{A}=\frac{{S}_{A}}{{V}_{A}}=\frac{\sqrt[]{100+{x}^{2}}}{4}](/latexrender/pictures/925478060ab90bbcd58c646cbb48e243.png)
O tempo total é uma função de x:
![t(x)={t}_{T}+{t}_{A}=10-\frac{1x}{10}+\frac{\sqrt[]{100+{x}^{2}}}{4} t(x)={t}_{T}+{t}_{A}=10-\frac{1x}{10}+\frac{\sqrt[]{100+{x}^{2}}}{4}](/latexrender/pictures/e9773eeff321b2072fe01e16265c2ce8.png)
Era necessário encontrar o ponto de mínimo absoluto dessa função, ou seja, o ponto em que o cão pulou na água realizando o menor tempo possível. Para isso, deriva-se a função:
![t'(x)=-\frac{1}{10}+\frac{x}{4\sqrt[2]{100+{x}^{2}}} t'(x)=-\frac{1}{10}+\frac{x}{4\sqrt[2]{100+{x}^{2}}}](/latexrender/pictures/abe774ac9eb2779bace675201603b704.png)
Para saber o mínimo absoluto a derivada tem que ser igual a ZERO, logo:
![t'(x)=0\Rightarrow-\frac{1}{10}+\frac{x}{4\sqrt[2]{100+{x}^{2}}}=0\Rightarrow\frac{1}{10}=\frac{x}{4\sqrt[2]{100+{x}^{2}}}\Rightarrow x=\frac{20}{\sqrt[]{21}} t'(x)=0\Rightarrow-\frac{1}{10}+\frac{x}{4\sqrt[2]{100+{x}^{2}}}=0\Rightarrow\frac{1}{10}=\frac{x}{4\sqrt[2]{100+{x}^{2}}}\Rightarrow x=\frac{20}{\sqrt[]{21}}](/latexrender/pictures/111d6ae2fd51470b3feda249f36d6e8a.png)
Este é um ponto de mínimo local e absoluto, pois a
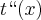 (segunda derivada) é igual a
(segunda derivada) é igual a 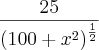 que é maior que ZERO
que é maior que ZERO 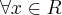 . Logo o gráfico é côncavo para cima e no ponto
. Logo o gráfico é côncavo para cima e no ponto ![x=\frac{20}{\sqrt[]{21}} x=\frac{20}{\sqrt[]{21}}](/latexrender/pictures/245f8f9c07b997b0566b01ac544863a5.png) ocorre
ocorre 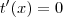 , o que garante que
, o que garante que ![x=\frac{20}{\sqrt[]{21}} x=\frac{20}{\sqrt[]{21}}](/latexrender/pictures/245f8f9c07b997b0566b01ac544863a5.png) é o ponto onde ocorre o valor mínimo absoluto.
é o ponto onde ocorre o valor mínimo absoluto.Agora o mais impressionante:
![\frac{20}{\sqrt[]{21}}=4,364357... \frac{20}{\sqrt[]{21}}=4,364357...](/latexrender/pictures/4f8de3f5d5ee04436185cec95c73a61d.png)
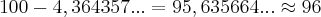






 , avisa que eu resolvo.
, avisa que eu resolvo.

