Pensando e esboçando gráficos

por **admin** » Qui Mar 06, 2008 17:21

Olá!

Farei um breve comentário sobre alguns procedimentos importantes e elementares que auxiliam o entendimento de gráficos de muitas funções.

Para começar, faça uma pausa e tente responder esta pergunta: como você traça o gráfico de uma reta?
Pense e tenha o seu método em mente.

No caso de retas, há várias formas, mas acredito que se você fizer uso do que eu tentarei explicar, conseguirá esboçar muitos gráficos mentalmente, apenas olhando para suas equações.

A idéia é partir do exemplo mais simples da classe de funções.
Para retas, comece pela bissetriz dos quadrantes ímpares:

y = x

Sempre quando for traçar um gráfico de reta, comece por esta.

Em seguida, obedecendo a precedência de operações, aplique à reta a variação do fator

( $a \in \Re$ ):

y = ax

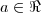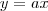
Repare que o fator

causará uma variação na inclinação da reta, mantendo a origem fixa no ponto (0, 0):
Se a > 1

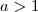, aumentará o ângulo da reta com o eixo

.
Se

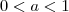, diminuirá o ângulo da reta com o eixo

.
Se

, primeiro, faça a reflexão da reta no eixo

, depois a respectiva variação do ângulo, analogamente aos dois casos anteriores.

Na prática, para você encontrar de quanto foi a variação, utilize o ponto (1, 1) por onde a reta está passando.
Após a multiplicação, a reta passará pelo ponto (1, a).

E por fim, trate uma eventual variação da parcela

( $b \in \Re$ ):
y = ax + b

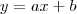
Veja que

fará a reta atual "subir" ou "descer" no plano, dependendo do sinal.
Pense na reta como um "objeto rígido" e faça estas variações "manualmente".
Se estiver na lousa, pegue uma régua e faça acreditar que a régua é a reta!
Mexa a régua conforme variar a reta!

Se b > 0

, suba a origem da reta até

no eixo

(repare que o "objeto" inteiro subirá

, ponto a ponto).
Se b < 0

, desça a origem da reta até

correspondente no eixo

(o "objeto" inteiro descerá

, ponto a ponto).
Veja que da origem anterior em (0, 0), obtivemos um novo ponto (0,b).

Pronto! A reta está na posição certa!
O gráfico está traçado!

No meu caso, estes procedimentos não foram ensinados no ensino médio.
Embora sejam bem elementares e excelentes para visualização, em geral não são utilizados.
Os créditos são da professora Barufi IME-USP.

É muito comum traçarem retas a partir de dois pontos, fazendo a chamada "tabelinha".
Os professores nunca deveriam favorecer este método.

Para se aprofundar neste assunto, recomendo o seguinte livro:

BARUFI, Maria Cristina Bonomi e LAURO, Maira Mendias. Funções elementares, equações e inequações: uma abordagem utilizando microcomputador. São Paulo: CAEM-IME/USP.

A mesma idéia você pode utilizar com outras classes de funções, por exemplo, o próximo passo é compreender as variações das parábolas, partindo de:
y = x^2

Depois, você pode estudar as variações das hipérboles, partindo de:
$y = \frac{1}{x}$

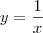
E outras, como:
$y = \sqrt{x}$

$y = ln\;x$

y = e^x

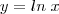
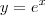
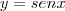
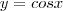
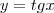
etc.

Assim, inclusive, você se habitua a identificar qual o tipo de gráfico que uma função mais simples possui, apenas olhando para sua equação e identificando sua classe. Depois, faça as variações!

O processo é muito rápido mentalmente e traz vários benefícios matemáticos.
Se o aluno entender, ele vai sempre saber!

Para o estudo e visualização destas variações, eu sugiro o software WINPLOT, uma simples e poderosa ferramenta, disponível para download aqui:
http://math.exeter.edu/rparris/peanut/wppr32z.exe