MAT0130
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Crist » Sex Mar 15, 2013 21:43
por Crist » Sex Mar 15, 2013 21:43
Preciso resolver o PVI utilizando o método de separação de variáveis para encontrar a solução geral.
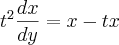
x(-1) =-1
por favor alguém me ajude , não consigo nem começar, pois tentei dividir por t^2, mas não sei se posso

-
Crist
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Out 24, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Mar 16, 2013 14:34
por e8group » Sáb Mar 16, 2013 14:34
Bom ainda não estudei equações diferenciais ,mas vou tentar ,qualquer erro na resolução post por favor.
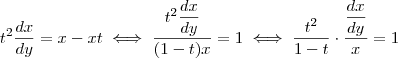
Daí integrando ambos membros com relação a

,obtemos :

.
A integral do membro à esquerda da igualdade não sei resolver .Se conseguir post .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Equações Diferenciais Ordinárias e Aplicações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- separação de variáveis
por Thais Bomfim » Qua Dez 12, 2012 14:07
- 3 Respostas
- 2332 Exibições
- Última mensagem por Thais Bomfim

Qui Dez 13, 2012 00:22
Equações
-
- Separação de variáveis e Integração
por Jhenrique » Qui Mai 09, 2013 20:34
- 6 Respostas
- 3623 Exibições
- Última mensagem por Jhenrique

Sáb Mai 11, 2013 15:36
Cálculo: Limites, Derivadas e Integrais
-
- Integral com separação de variáveis
por fernando ribeiro » Seg Nov 16, 2015 23:56
- 0 Respostas
- 1890 Exibições
- Última mensagem por fernando ribeiro

Seg Nov 16, 2015 23:56
Cálculo: Limites, Derivadas e Integrais
-
- [sistema com 2 variáveis]
por Zeh Edu » Ter Mai 08, 2012 01:54
- 0 Respostas
- 1217 Exibições
- Última mensagem por Zeh Edu

Ter Mai 08, 2012 01:54
Sistemas de Equações
-
- Função com 3 variáveis
por dina ribeiro » Sáb Jun 09, 2012 18:14
- 1 Respostas
- 1519 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 09, 2012 19:25
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
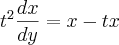

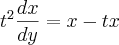

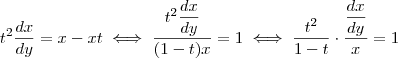
 ,obtemos :
,obtemos :  .
. 