MAT0120
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Cicero ferreira » Sex Mar 14, 2014 18:13
por Cicero ferreira » Sex Mar 14, 2014 18:13
Determinar o valor de k para que o vetor
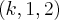
pertença ao plano

determinado pela equação cartesiana
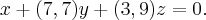
-
Cicero ferreira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 04, 2014 13:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
Voltar para Álgebra I para Licenciatura
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- subespaço gerado
por Cicero ferreira » Sex Mar 14, 2014 18:23
- 1 Respostas
- 1553 Exibições
- Última mensagem por Russman

Sex Mar 14, 2014 23:00
Introdução à Álgebra Linear
-
- Subespaço gerado
por drleonunes » Qui Abr 16, 2015 21:10
- 0 Respostas
- 1516 Exibições
- Última mensagem por drleonunes

Qui Abr 16, 2015 21:10
Álgebra Linear
-
- Álgebra linear - Subespaço Gerado
por nietzsche » Sex Jan 06, 2012 19:48
- 2 Respostas
- 1908 Exibições
- Última mensagem por nietzsche

Ter Jan 10, 2012 17:16
Álgebra Linear
-
- [Subespaço R^4]Vetores LD
por guisaulo » Qui Nov 29, 2012 12:36
- 1 Respostas
- 2335 Exibições
- Última mensagem por MarceloFantini

Sex Nov 30, 2012 00:13
Álgebra Linear
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10977 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
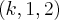 pertença ao plano
pertença ao plano  determinado pela equação cartesiana
determinado pela equação cartesiana 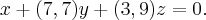

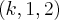 pertença ao plano
pertença ao plano  determinado pela equação cartesiana
determinado pela equação cartesiana