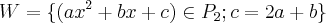 é um subespaço vetorial de
é um subespaço vetorial de 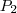 , o conjunto dos polinômios de grau menor ou igual a 2.
, o conjunto dos polinômios de grau menor ou igual a 2.
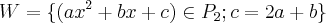 é um subespaço vetorial de
é um subespaço vetorial de 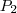 , o conjunto dos polinômios de grau menor ou igual a 2.
, o conjunto dos polinômios de grau menor ou igual a 2.

 . Daí,
. Daí,  é da forma
é da forma  , onde
, onde  . Queremos saber se
. Queremos saber se 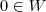 . Para tanto, temos que verificar se
. Para tanto, temos que verificar se  . Assim, consideremos
. Assim, consideremos  . Então, podemos partir então para a próxima etapa:
. Então, podemos partir então para a próxima etapa:
 , então
, então  );
); ,
,  ;
;
 é um ESPAÇO vetorial, de fato. Agora, para mostrar que o mesmo é SUBespaço de
é um ESPAÇO vetorial, de fato. Agora, para mostrar que o mesmo é SUBespaço de 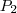 precisamos mostrar que
precisamos mostrar que  .
. , podemos tomar
, podemos tomar  nesse espaço ( como a e b são reais,uma combinação linear deles também o é) e então este será confundido com
nesse espaço ( como a e b são reais,uma combinação linear deles também o é) e então este será confundido com  . Assim, podemos "achar"
. Assim, podemos "achar"  "dentro" de
"dentro" de 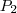 . Portanto, é subespaço.
. Portanto, é subespaço.
Russman escreveu:Perfeito. Você mostrou queé um ESPAÇO vetorial, de fato. Agora, para mostrar que o mesmo é SUBespaço de
precisamos mostrar que
.
Como, podemos tomar
nesse espaço ( como a e b são reais,uma combinação linear deles também o é) e então este será confundido com
. Assim, podemos "achar"
"dentro" de
. Portanto, é subespaço.



 , por exemplo, satisfaz todos os requerimentos de espaço vetorial e não é subespaço de
, por exemplo, satisfaz todos os requerimentos de espaço vetorial e não é subespaço de  .
.
Voltar para Introdução à Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
