eu já olhei alguns tópicos de espaço e subspaço vetorial (que me ajudaram mto) mas mesmo assim estou tendo dificuldade com um exercício que envolve números complexos... não sei como verificar os axiomas por causa da parte imaginária. :(
o exercício é o seguinte:
Seja V= {(x,y)| x,y
 C}. Mostre que V é um espaço vetorial sobre R com a adição e multiplicação por escalares definida como:
C}. Mostre que V é um espaço vetorial sobre R com a adição e multiplicação por escalares definida como:I) (x1, y1) + (x2,y2) = (x1+x2, y1+y2),
 (x1,y1) e (x2,y2)
(x1,y1) e (x2,y2)  V;
V;II) a (x,y) = (ax, ay),
 a
a  R e
R e  (x, y)
(x, y)  V.
V.Obrigada.


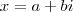 e
e 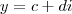 (onde
(onde 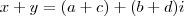 . Já o produto kx (com k um escalar), definimos como
. Já o produto kx (com k um escalar), definimos como 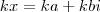 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)