MAP0151
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por zifles2012 » Seg Set 17, 2012 16:13
por zifles2012 » Seg Set 17, 2012 16:13
De acordo com o método de Newton descubra as raizes da função
- Código: Selecionar todos
[tex]x^2+lnx = 0[/tex]
Eu queria saber apenas por onde começar.. obrigado
-
zifles2012
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Set 17, 2012 16:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por LuizAquino » Seg Set 17, 2012 19:55
por LuizAquino » Seg Set 17, 2012 19:55
zifles2012 escreveu:De acordo com o método de Newton descubra as raizes da função
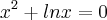
Eu queria saber apenas por onde começar.. obrigado
Você já deve saber que o Método de Newton tem o seguinte formato:
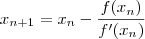
Analisando a equação dada (que foi
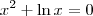
), podemos criar a função
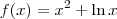
. O objetivo é determinar a raiz (ou raízes) dessa função. Ou seja, o valor de x tal que f(x) = 0.
Você já deve saber que
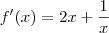
. Desse modo, você terá o esquema:
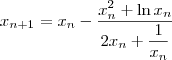
Agora escolha um chute inicial

e efetue o processo iterativo quantos passos desejar. Por exemplo, você pode parar em um passo
k tal que
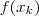
seja tão próximo de zero quanto você deseja.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo Numérico e Aplicações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [InduçãoMatemática] Duvida nessa questão!!
 por juliohenriquelima14 » Ter Nov 04, 2014 11:24
por juliohenriquelima14 » Ter Nov 04, 2014 11:24
- 6 Respostas
- 3304 Exibições
- Última mensagem por juliohenriquelima14

Ter Nov 04, 2014 16:28
Equações
-
- [Derivadas]Duvida nessa questão
por Flavio50 » Dom Abr 19, 2015 12:45
- 2 Respostas
- 1886 Exibições
- Última mensagem por Flavio50

Seg Abr 27, 2015 13:47
Cálculo: Limites, Derivadas e Integrais
-
- [Método de Newton] em função 2/x
por BNK » Sáb Mai 12, 2012 12:32
- 4 Respostas
- 2069 Exibições
- Última mensagem por BNK

Seg Mai 14, 2012 18:02
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo numérico, metodo de newton
por Crist » Qua Out 30, 2013 16:47
- 4 Respostas
- 3503 Exibições
- Última mensagem por Crist

Sex Nov 01, 2013 13:46
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Numérico] Método de Newton
por joaofernandes » Dom Jun 19, 2016 19:51
- 0 Respostas
- 1483 Exibições
- Última mensagem por joaofernandes

Dom Jun 19, 2016 19:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


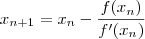
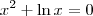 ), podemos criar a função
), podemos criar a função 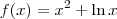 . O objetivo é determinar a raiz (ou raízes) dessa função. Ou seja, o valor de x tal que f(x) = 0.
. O objetivo é determinar a raiz (ou raízes) dessa função. Ou seja, o valor de x tal que f(x) = 0.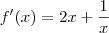 . Desse modo, você terá o esquema:
. Desse modo, você terá o esquema: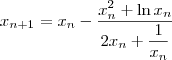
 e efetue o processo iterativo quantos passos desejar. Por exemplo, você pode parar em um passo k tal que
e efetue o processo iterativo quantos passos desejar. Por exemplo, você pode parar em um passo k tal que 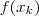 seja tão próximo de zero quanto você deseja.
seja tão próximo de zero quanto você deseja.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
