Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Molina » Qui Nov 25, 2010 17:00
por Molina » Qui Nov 25, 2010 17:00
Boa tarde!
Encontrei este desafio pelos corredores da universidade e já aviso que não tenho a resposta. Então seria interessante debatermos sobre o problema, aí vai:
O número 111...10888...89 com n algarismos 1 e n algarismos 8 é um quadrado perfeito? 

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por victoreis1 » Qui Nov 25, 2010 18:13
por victoreis1 » Qui Nov 25, 2010 18:13
3 x 3 = 09 (0 algarismos 1 e 0 algarismos 8)
33 x 33 = 1089 (1 algarismo 1 e 1 algarismo 8)
333 x 333 = 110889 (2 algarismos 2 e 2 algarismos 8)
333.. (n vezes 3) x 333.. (n vezes 3) = 11...088...9 (n-1 algarismos 1 e n-1 algarismos 8)
que tipo de prova ele pede; tem que usar aritmética modular, ou pode ser por indução mesmo?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Nov 25, 2010 18:16
por Molina » Qui Nov 25, 2010 18:16
Ninguém pede nada, Victor.
Mas por ser n natural acredito que saia por indução mesmo...

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Renato_RJ » Qui Jan 06, 2011 16:25
por Renato_RJ » Qui Jan 06, 2011 16:25
Se o problema é sobre quadrados perfeitos, acredito que tenhamos que utilizar congruência... Além de que, os quadrados perfeitos quando divididos por 3 ou 4 apresentam restos 1 ou 0.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Otavio Rubiao » Seg Fev 07, 2011 09:26
por Otavio Rubiao » Seg Fev 07, 2011 09:26
Se ainda estiverem interessados na resolução:
Escrevendo os termos do numero 111...1088...89 como a soma de outro numeros temos:
111..11000..00 onde (11...11) = n numeros e (000....000) = n + 2
888...880 onde (888...8) = n
percebemos que o primeiro e o segundo numeros podem ser escritos com a soma de uma PG:
1.10^n+2 + 10.10^n+2 + 100.10^n+2 +...+ 10^2n+1 = 10^n+2.(10^n - 1)/10 - 1
80 + 800 + 8000 +...+ 8.10^n = 80.( 10^n - 1)/10 - 1
9 = 9
logo: 1111...10888....89 = (10^2n+2 - 10^n+2 + 80.10^n - 80 + 81)/9 desenvolvendo :
111...10888...89 = ((10^n+1 - 1)/3)² C.Q.D
-
Otavio Rubiao
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jan 27, 2011 10:24
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por pedroaugustox47 » Sex Mai 11, 2012 16:28
por pedroaugustox47 » Sex Mai 11, 2012 16:28
simples representação decimal:
.

.

.

.
![\frac{\left[ 10^\left(2n+2 \right) \right] - \left[ 10^\left(n+2 \right) \right]+\left[80.10^n \right]+1}{9}= \frac{\left[ 10^\left(2n+2 \right) \right] - \left[ 10^\left(n+2 \right) \right]+\left[80.10^n \right]+1}{9}=](/latexrender/pictures/c9da60c6e1dfad77d6056dd7a0cba5f4.png)
.
![\frac{\left[ \left(10^\left(n+1 \right) \right)^2 \right] -100.10^n +80.10^n+1}{9}= \frac{\left[ \left(10^\left(n+1 \right) \right)^2 \right] -100.10^n +80.10^n+1}{9}=](/latexrender/pictures/88c6f1e0dce10bd07c96ab3c8276109a.png)
.
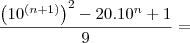
.
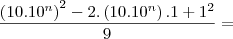
.
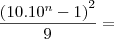
.
![\left( \frac{\left[10^\left(n+1 \right) \right]-1}{3} \right)^2 \left( \frac{\left[10^\left(n+1 \right) \right]-1}{3} \right)^2](/latexrender/pictures/414519d556d9894bbcfe7a88f647a9f1.png)
...... C.Q.D
.
abraços

-
pedroaugustox47
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Mai 11, 2012 01:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Sistema Elite de Ensino-CN/EPCAR
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3744 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
-
- Quadrado perfeito
por guillcn » Ter Abr 05, 2011 19:15
- 2 Respostas
- 2506 Exibições
- Última mensagem por guillcn

Ter Abr 05, 2011 19:54
Álgebra Elementar
-
- Ajuda com quadrado perfeito
por joaoalbertotb » Ter Ago 25, 2009 13:01
- 2 Respostas
- 2299 Exibições
- Última mensagem por joaoalbertotb

Qua Ago 26, 2009 12:20
Trigonometria
-
- Trinômio Quadrado Perfeito
por Balanar » Ter Ago 10, 2010 22:48
- 2 Respostas
- 4914 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 18:05
Desafios Difíceis
-
- Dúvida em polinômio com quadrado perfeito
por Nerd » Seg Set 03, 2012 22:07
- 1 Respostas
- 2045 Exibições
- Última mensagem por Russman

Seg Set 03, 2012 23:05
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.















![\frac{\left[ 10^\left(2n+2 \right) \right] - \left[ 10^\left(n+2 \right) \right]+\left[80.10^n \right]+1}{9}= \frac{\left[ 10^\left(2n+2 \right) \right] - \left[ 10^\left(n+2 \right) \right]+\left[80.10^n \right]+1}{9}=](/latexrender/pictures/c9da60c6e1dfad77d6056dd7a0cba5f4.png)
![\frac{\left[ \left(10^\left(n+1 \right) \right)^2 \right] -100.10^n +80.10^n+1}{9}= \frac{\left[ \left(10^\left(n+1 \right) \right)^2 \right] -100.10^n +80.10^n+1}{9}=](/latexrender/pictures/88c6f1e0dce10bd07c96ab3c8276109a.png)
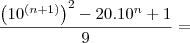
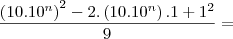
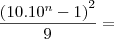
![\left( \frac{\left[10^\left(n+1 \right) \right]-1}{3} \right)^2 \left( \frac{\left[10^\left(n+1 \right) \right]-1}{3} \right)^2](/latexrender/pictures/414519d556d9894bbcfe7a88f647a9f1.png) ...... C.Q.D
...... C.Q.D


 .
.
 :
: