Olá, Fábio Chagas!
Considero que a dificuldade deste exercício está em dois aspectos: a abstração para representá-lo geometricamente e a escolha de um cálculo que leve à resolução.
Outros comentários sobre a interpretação do enunciado:
A unidade de "distância" adotada é a "remada".
E a informação de que o lenhador "remava regularmente" significa então que a velocidade é constante. Neste caso, vale ressaltar que a velocidade é a variação das remadas no tempo.
E este trecho: "um peixe irrompeu à superfície bem à sua frente", em outras palavras, significa que o ponto do peixe está alinhado com o trajeto do lenhador.
E este outro: "tranqüilo lago", transmite a idéia de que a propagação das ondulações também é constante.
Pois bem, após estas considerações, o primeiro passo então é fazer uma representação geométrica, por exemplo, eu fiz esta:
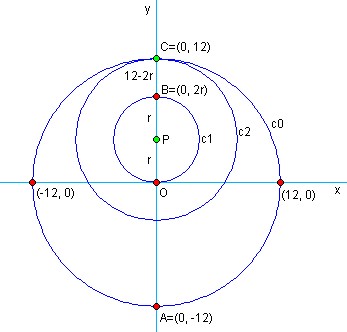
- desafio_lenhador.jpg (21.23 KiB) Exibido 2990 vezes
O lenhador vai no sentido AC.
Sendo que o ponto A representa a posição do lenhador no exato momento inicial de formação das ondulações.
Conforme o enunciado, o ponto O é a posição de encontro com o primeiro círculo c1 formado.
E o ponto C é a posição de saída do círculo correspondente c2.
O raio do círculo c1 é r.
A medida da distância BC assinalada como 12-2r é proveniente da diferença OC-OB (OC menos o diâmetro de c1).
Citei inicialmente a escolha do cálculo como dificuldade pois, unindo alguns pontos das intersecções das circunferências com o eixo x, podemos criar vários triângulos, alguns triângulos retângulos inclusive. Então, é natural buscarmos uma resolução geométrica, por exemplo, com semelhança de triângulos, teorema de Pitágoras etc.
Mas, é fato que o enunciado estabelece uma relação entre as remadas e a propagação das ondas.
Sendo assim, buscando simplificar, relacionei as remadas com o raio de c1, através de uma regra de três.
A idéia:

Em palavras, esta regra de três representa o seguinte:
O lenhador percorre AO, proporcionalmente à propagação PB. Asim como percorre OC, proporcionalmente à propagação BC.
A conta:
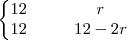
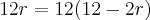

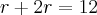
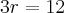

E como procuramos a distância AP, temos:
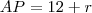
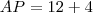

remadas
Qualquer comentário será bem-vindo!
Até mais.





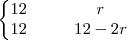
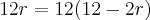

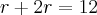
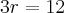

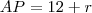
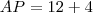
 remadas
remadas
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.