Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Taah » Dom Mar 28, 2010 13:39
por Taah » Dom Mar 28, 2010 13:39
Calcule sin(x+y) em função de
a e
b, sabendo que o produto
ab
0, que sinx + siny =
a e que cosx + cosy =
b
-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
 por Elcioschin » Dom Mar 28, 2010 18:07
por Elcioschin » Dom Mar 28, 2010 18:07
senx + seny = a ----> 2*sen[(x + y)/2]*cos[(x - y)/2] = a ----> I
cosx + cosy = b ----> 2*cos[(x + y)/2]*cos[(x - y)/2] = b ----> II
I : II ----> sen[(x + y)/2]/cos[(x + y)/2] = a/b ----> sen²[(x + y)/2]/cos²[(x + y)/2] = a²/b² ----> sen²[(x + y)/2]/{1 - sen²[(x + y)/2]} = a²/b² ---->
b²*sen²[(x + y)/2] = a² - a²*sen²[(x + y)/2] ----> sen²[(x + y)/2] = a²/(a² + b²) ---->sen[(x + y)/2] = a/V(a² + b²) ----> III
sen(x + y) = sen[(x + y)/2 + sen(x + y)/2] ----> sen(x + y) = 2*sen[(x + y)/2]*cos[(x + y)/2] ----> sen²(x + y) = 4*sen²[(x + y)/2]*cos²[(x + y)/2] ---->
sen²(x + y) = 4*sen²[(x + y)/2]*{1 - sen²[(x + y)/2]} ----> sen²(x + y) = 4*sen²[(x + y)/2] - 4*{sen²[(x + y)/2]}² ----> IV
III em IV -----> sen²(x + y) = 4*[a²/(a² + b²)] - 4*[a²/(a² + b²)]² ----> sen²(x + y) = 4a²/(a² + b²) - 4*a^4/(a² + b²)² ----> sen²(x + y) = [4a²*(a² + b²) - 4a^4]/(a² + b²)²
sen²(x+ y) = 4a²b²/(a² + b²)² ----> sen(x + y)= 2ab/(a² + b²)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Taah » Seg Mar 29, 2010 14:44
por Taah » Seg Mar 29, 2010 14:44
E se eu fizesse:
sen(x+y)= ?
senx + seny = a
cosx + cosy = b
a = 2.sen
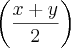
.cos
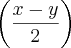
b = 2.cos
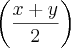
.cos
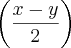

_________________________________________________________________________
a + b = 2.sen
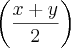
.cos
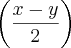
+ 2.cos
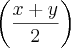
.cos
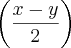
a + b = 2.cos
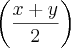
.
![\left[ \left(sen. \frac{x+y}{2} \right)+ cos.\left( \frac{x+y}{2} \right) \right] \left[ \left(sen. \frac{x+y}{2} \right)+ cos.\left( \frac{x+y}{2} \right) \right]](/latexrender/pictures/4cd1be5c601bacb99447e0751f0d9286.png)
Elevando ambos os lados ao quadrado:
a² + 2ab + b² = 4.cos²
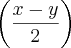
.
![\left[ sen²\left( \frac{x+y}{2} \right) + 2.sen\left( \frac{x+y}{2 \right)}.cos\left( \frac{x+y}{2} \right) + cos²\left( \frac{x+y}{2} \right) \right] \left[ sen²\left( \frac{x+y}{2} \right) + 2.sen\left( \frac{x+y}{2 \right)}.cos\left( \frac{x+y}{2} \right) + cos²\left( \frac{x+y}{2} \right) \right]](/latexrender/pictures/9256f791c89fea4e727c7685ad5c5d49.png)
a² + 2ab + b² =
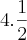
.
![\left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right] \left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right]](/latexrender/pictures/d3e7820f5bb73b10a324221425b868fe.png)
2.
![\left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right] = a² + 2ab + b² \left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right] = a² + 2ab + b²](/latexrender/pictures/dd6a1504ab046b0d317126ce5dd49b1d.png)
![1 + sen(x+y) = \frac{a² + 2ab + b²}{2. \left[ cos(x-y) + 1 \right]} 1 + sen(x+y) = \frac{a² + 2ab + b²}{2. \left[ cos(x-y) + 1 \right]}](/latexrender/pictures/5fccca899f01852dfd6dc693839f6718.png)
![sen(x+y) = \frac{a²+ 2ab + b²}{2.\left[ cos(x-y) + 1 \right]} sen(x+y) = \frac{a²+ 2ab + b²}{2.\left[ cos(x-y) + 1 \right]}](/latexrender/pictures/3ff86814a39370cdcd6c4eabcf83f2bf.png)
Nossos resultados divergem entre si!
E agora???
-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
 por Elcioschin » Seg Mar 29, 2010 15:54
por Elcioschin » Seg Mar 29, 2010 15:54
1) Primeiramente existe um erro na 4ª linha----> a + b = 2*cos[(x - y)/2]*[ ..... ----> O sinal deveria ser de subtração. Na próxima linha vc já corrigiu.
2) Em segndo lugar vc escreveu no final ----> a² + 2ab + b² = a*² + ab + b² ----> Não entendí nada! O que é ² ? Suponho qe seja do LaTeX.
3) A sua solução DEVERIA ser função somente de a, b (conforme enunciado) e vc deixou em função de cos(x - y) e deste tal ²
Assm vc não chegou numa solução válida e, portanto, não pode comparar com a minha solução.
Finalmente, para confirmar que minha solução está correta, faça um teste:
Faça, por exemplo x = 30º e y = 60º
Calcule a, b
Calcule sen(x + y), usando a fórmula que eu deduzí.
Calcule sen(x + y) diretamente, substituindo pelos valores dados.
Compare as duas soluções.
Se quiser, escolha outros valores de x, y e faça o mesmo (por exemplo x = 45º e y = 45º)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Taah » Seg Mar 29, 2010 16:02
por Taah » Seg Mar 29, 2010 16:02
Brigada!
To errada.. o tal A^ q aparece aí é do editor msm! Hehe
Mas olha, em relação ao teu cálculo
Poderias então me explicar o como dezenvolvesse a 4ª linha do teu cálculo?
Por favor... Vlw!
-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
 por Elcioschin » Seg Mar 29, 2010 16:13
por Elcioschin » Seg Mar 29, 2010 16:13
Nas duas primeiras linhas simplesmente transformei as somas em produtos (Fómula básica da trigonometria: pesquise)
Depois dividí uma equação pela outra e fiz mudanças simples de membros, até chegar em III
Depois usei a fórmula do arco metade ----> sen(2m) = sen(m + m) = 2*sen(m/2)*cos(m/2) fazendo m = (x + y)/2
Mais algumas simplificaçõe algébricas até chegar em IV
Depois substituí III em IV e mais algumas transforações simples
Leia com cuidado, ou melhor escreva vc pessoalmente que entenderá.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Taah » Seg Mar 29, 2010 16:36
por Taah » Seg Mar 29, 2010 16:36
Olá novamente!
Desde o princípio venho escrevendo o seu cálculo, porém (creio que já esteja cansada!) não consigo compreender como voce chegou a colocar a²+b² como divisores da questão.
Parece-me que essas suas modificações simples não são tão simples para mim.
Seria de muito abuso me descrever suas mudanças simples de membro até chegar em a²+b² como divisores?
Desde já agradeço!
-
Taah
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Mar 27, 2010 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Exatas
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de sin(x+y) UMA MANEIRA FÁCIL DE RESOLVER
por Taah » Ter Mar 30, 2010 09:02
- 1 Respostas
- 6520 Exibições
- Última mensagem por paulo87

Sáb Fev 19, 2011 12:26
Desafios Difíceis
-
- XD parece impossível
por Fernanda Lauton » Ter Jun 29, 2010 10:35
- 3 Respostas
- 1975 Exibições
- Última mensagem por Fernanda Lauton

Qui Jul 01, 2010 08:47
Logaritmos
-
- Nível fácil - FCC e UPE
por ingridgusmao » Dom Jun 12, 2011 02:41
- 1 Respostas
- 7521 Exibições
- Última mensagem por nietzsche

Sex Jun 24, 2011 22:54
Conjuntos
-
- Radiciação (fácil)
por TAE » Sex Mai 11, 2012 18:15
- 2 Respostas
- 1467 Exibições
- Última mensagem por TAE

Sáb Mai 12, 2012 16:38
Álgebra Elementar
-
- dúvida fácil
por TAE » Ter Mai 22, 2012 21:04
- 3 Respostas
- 1949 Exibições
- Última mensagem por DanielFerreira

Qui Mai 24, 2012 11:04
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 0, que sinx + siny = a e que cosx + cosy = b
0, que sinx + siny = a e que cosx + cosy = b

 0, que sinx + siny = a e que cosx + cosy = b
0, que sinx + siny = a e que cosx + cosy = b

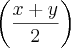 .cos
.cos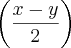
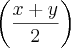 .cos
.cos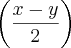

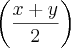 .cos
.cos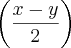 + 2.cos
+ 2.cos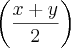 .cos
.cos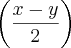
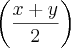 .
.![\left[ \left(sen. \frac{x+y}{2} \right)+ cos.\left( \frac{x+y}{2} \right) \right] \left[ \left(sen. \frac{x+y}{2} \right)+ cos.\left( \frac{x+y}{2} \right) \right]](/latexrender/pictures/4cd1be5c601bacb99447e0751f0d9286.png)
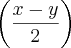 .
.![\left[ sen²\left( \frac{x+y}{2} \right) + 2.sen\left( \frac{x+y}{2 \right)}.cos\left( \frac{x+y}{2} \right) + cos²\left( \frac{x+y}{2} \right) \right] \left[ sen²\left( \frac{x+y}{2} \right) + 2.sen\left( \frac{x+y}{2 \right)}.cos\left( \frac{x+y}{2} \right) + cos²\left( \frac{x+y}{2} \right) \right]](/latexrender/pictures/9256f791c89fea4e727c7685ad5c5d49.png)
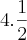 .
.![\left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right] \left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right]](/latexrender/pictures/d3e7820f5bb73b10a324221425b868fe.png)
![\left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right] = a² + 2ab + b² \left[ cos.(x-y) + 1 \right].\left[ 1 + sen.(x+y) \right] = a² + 2ab + b²](/latexrender/pictures/dd6a1504ab046b0d317126ce5dd49b1d.png)
![1 + sen(x+y) = \frac{a² + 2ab + b²}{2. \left[ cos(x-y) + 1 \right]} 1 + sen(x+y) = \frac{a² + 2ab + b²}{2. \left[ cos(x-y) + 1 \right]}](/latexrender/pictures/5fccca899f01852dfd6dc693839f6718.png)
![sen(x+y) = \frac{a²+ 2ab + b²}{2.\left[ cos(x-y) + 1 \right]} sen(x+y) = \frac{a²+ 2ab + b²}{2.\left[ cos(x-y) + 1 \right]}](/latexrender/pictures/3ff86814a39370cdcd6c4eabcf83f2bf.png)










