Ajudou Por Favor

[Midelio12]

Responde Esses perguntas

[Gebe]

Cara, divide o problema em mais de um topico e tenta seguir ao maximo as regras do forum, colocando duvidas mais detalhadas alem das suas tentativas/dificuldades, por exemplo.
Lembre-se que o objetivo do forum não é resolver listas de exercicios.
Pra não parecer má vontade em ajudar vou resolver as letras 'a' e 'b' da primeira questão.

Lembre-se que a equação da reta quando são dados dois pontos pode ser determinada por:
(y2 - y1) = m . (x2 - x1)

Onde x1 e y2 e x2 e y2 são as cordenadas dos dois pontos e 'm' é o coeficiente angular (ou declive da reta).
Dito isso temos:

a) x1 = 1 , x2 = -3 , y1 = 2 , y2 = 2
(2 - 2) = m . (-3 - 1) --> m = 0
Reta com inclinação nula.

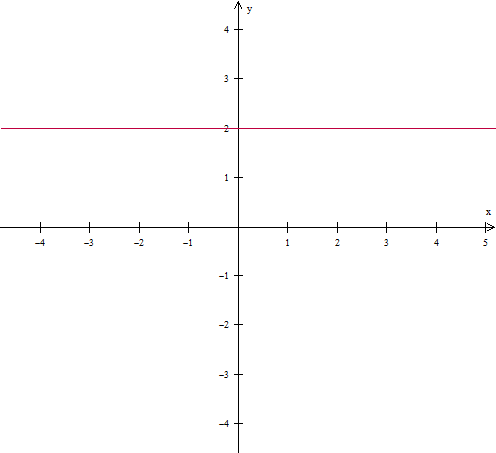
letra a.png (7.15 KiB) Exibido 14726 vezes

b) x1 = -1 , x2 = -3 , y1 = 0 , y2 = -2
(-2 - 0) = m . (-3 - (-1) )
m = -2/-2
m = 1
Reta com inclinação unitaria

letra b.png (7.68 KiB) Exibido 14726 vezes