Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por henrique25 » Ter Dez 14, 2010 13:15
por henrique25 » Ter Dez 14, 2010 13:15
demonstre que cada wff é um teorema da logica dos prodicados:
legenda: "e" = "^"
"ou"="^ invertido"
![1-(\forall x)P(x)\rightarrow(\forall x)[P(x) ou Q(x)] 1-(\forall x)P(x)\rightarrow(\forall x)[P(x) ou Q(x)]](/latexrender/pictures/b0e61d1f5ceecd48de1a5e3540ecb258.png)
![2-(\forall x)P(x) e (\exists x)Q(x)\rightarrow (\exists x)[P(x) e Q(x)] 2-(\forall x)P(x) e (\exists x)Q(x)\rightarrow (\exists x)[P(x) e Q(x)]](/latexrender/pictures/ad782706c6558aefd63c0e303cfa4e4c.png)
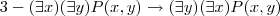
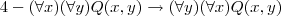
-
henrique25
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mai 08, 2010 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informatica
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 5793 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
-
- Lógica
por Neperiano » Qui Jun 19, 2008 16:48
- 17 Respostas
- 26835 Exibições
- Última mensagem por Neperiano

Sex Nov 11, 2011 15:51
Desafios Enviados
-
- lÓGICA
por Jaison Werner » Qui Set 15, 2011 11:28
- 2 Respostas
- 3637 Exibições
- Última mensagem por Neperiano

Qui Nov 10, 2011 15:31
Lógica e Conjuntos
-
- Lógica
por Pstefani » Ter Set 20, 2011 19:56
- 1 Respostas
- 2617 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 21:40
Sistemas de Equações
-
- [lógica]
por Ed_29 » Qui Ago 09, 2012 21:25
- 5 Respostas
- 7129 Exibições
- Última mensagem por fraol

Sáb Ago 11, 2012 16:09
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![1-(\forall x)P(x)\rightarrow(\forall x)[P(x) ou Q(x)] 1-(\forall x)P(x)\rightarrow(\forall x)[P(x) ou Q(x)]](/latexrender/pictures/b0e61d1f5ceecd48de1a5e3540ecb258.png)
![2-(\forall x)P(x) e (\exists x)Q(x)\rightarrow (\exists x)[P(x) e Q(x)] 2-(\forall x)P(x) e (\exists x)Q(x)\rightarrow (\exists x)[P(x) e Q(x)]](/latexrender/pictures/ad782706c6558aefd63c0e303cfa4e4c.png)
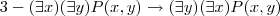
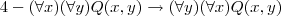

![1-(\forall x)P(x)\rightarrow(\forall x)[P(x) ou Q(x)] 1-(\forall x)P(x)\rightarrow(\forall x)[P(x) ou Q(x)]](/latexrender/pictures/b0e61d1f5ceecd48de1a5e3540ecb258.png)
![2-(\forall x)P(x) e (\exists x)Q(x)\rightarrow (\exists x)[P(x) e Q(x)] 2-(\forall x)P(x) e (\exists x)Q(x)\rightarrow (\exists x)[P(x) e Q(x)]](/latexrender/pictures/ad782706c6558aefd63c0e303cfa4e4c.png)
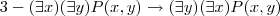
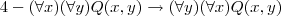

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)