A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por admin » Sex Jul 20, 2007 15:03
por admin » Sex Jul 20, 2007 15:03
Numa festinha de aniversário havia uma caixa de bombons para as crianças. Cada uma pegou 2 bombons e sobraram 5 na caixa. Se cada criança tivesse pego 3 bombons, uma ficaria sem. Pergunto: Quantas crianças havia na festa e quantos bombons havia na caixa?
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por heroncius » Qui Set 06, 2007 21:16
por heroncius » Qui Set 06, 2007 21:16
n° de crianças é 7 e o total de bombons,19...tah correto?!
-
heroncius
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Jul 31, 2007 11:22
 por admin » Sex Set 07, 2007 05:45
por admin » Sex Set 07, 2007 05:45
heroncius escreveu:n° de crianças é 7 e o total de bombons,19...tah correto?!
Olá
heroncius!
Não dizendo diretamente, porque isso seria menos importante, vou representar o enunciado através de um sistema de equações, ok? Assim, você verifica sua resposta.
Vou nomear as variáveis:
B: número de bombons
C: número de crianças
Cada uma pegou 2 bombons e sobraram 5 na caixa.
Deste trecho, temos que:
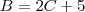
Se cada criança tivesse pego 3 bombons, uma ficaria sem.
E deste:

Então, temos um sistema com duas equações e duas incógnitas:
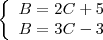
Depois que você encontrar os valores, pode testá-los no próprio enunciado.
Inclusive, também pode fazer isso com estes que você já havia encontrado.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por heroncius » Sex Set 07, 2007 11:38
por heroncius » Sex Set 07, 2007 11:38
valeu pelo esclercimento Fábio,
abraço!!!
-
heroncius
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Jul 31, 2007 11:22
 por Kiraxx » Qui Jun 19, 2008 02:02
por Kiraxx » Qui Jun 19, 2008 02:02
Fiz de cabeça mesmo, chutando valores aproximados... acho que tá certo...!
Primeiro eu pensei no número 10 para as crianças e não deu certo.
Depois pensei no 7 e cheguei quase lá.
Então cheguei no número 6. Com base nele pude chegar ao número 17 de bombons.
Eis a minha teoria:
Se 6 crianças pegam 2 bombons cada e ainda sobram 5, significa que haviam 17 bombons na caixa.
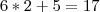
Se essas mesmas 6 crianças comessem 3 bombons cada, daria um total de 18 bombons, ou seja, uma criança ficaria sem.
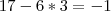
Sendo assim, haviam
6 crianças e
17 bombons na caixa.
Acertei?

-
Kiraxx
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 19, 2008 01:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Adm. - Comércio Exterior
- Andamento: cursando
 por admin » Qui Jun 19, 2008 02:26
por admin » Qui Jun 19, 2008 02:26
Olá, boas-vindas!
Vale ressaltar que o método de tentativas e erros é, em geral, ineficiente.
De qualquer forma, os valores não estão corretos.
Percebo que você está mal interpretando o trecho "uma ficaria sem".
Uma criança ficar sem bombom é diferente de faltar um bombom!
Sugiro não ignorar o sistema linear.
Para "chutes" não teríamos argumentos matemáticos justificativos, bem como a discussão seria desnecessária.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Kiraxx » Qui Jun 19, 2008 02:29
por Kiraxx » Qui Jun 19, 2008 02:29
Sendo assim, a primeira resposta dada ao problema está certa né!
Interpretei mal mesmo, rsrs...
Mas tá tranquilo, só queria me divertir um pouco...
Obrigado pela atenção!
-
Kiraxx
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 19, 2008 01:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Adm. - Comércio Exterior
- Andamento: cursando
 por admin » Qui Jun 19, 2008 02:36
por admin » Qui Jun 19, 2008 02:36
Olá, tudo bem, compreendo.
Aquela resposta também não está correta.
Repare que também falha na segunda parte do enunciado, faltariam 2 bombons, o que é diferente de "uma criança ficaria sem".
Se "uma ficaria sem", cada uma pegando 3, é necessário que faltem 3.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Kiraxx » Qui Jun 19, 2008 02:39
por Kiraxx » Qui Jun 19, 2008 02:39
Cara, eu tinha feito as equações e o sistema que você montou de cabeça, e tinha dado 8. Mas eu não quis acreditar no resultado.
Olhando bem é exatamente isso né.
Tá certo... interessante como a nossa mente nos engana de vez em quando...!
-
Kiraxx
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 19, 2008 01:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Adm. - Comércio Exterior
- Andamento: cursando
 por admin » Qui Jun 19, 2008 02:43
por admin » Qui Jun 19, 2008 02:43
Isso Kiraxx, havia 8 crianças e 21 bombons.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




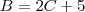

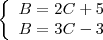


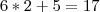
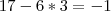






![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.