A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por alexandre32100 » Ter Nov 23, 2010 16:27
por alexandre32100 » Ter Nov 23, 2010 16:27
Que
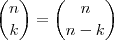
todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
-
alexandre32100
-
 por victoreis1 » Ter Nov 23, 2010 17:08
por victoreis1 » Ter Nov 23, 2010 17:08
usando a fórmula dá pra provar facilmente.. se vc construir o triângulo de pascal também..
como exatamente provar?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por alexandre32100 » Ter Nov 23, 2010 20:43
por alexandre32100 » Ter Nov 23, 2010 20:43
Usando a dialética (argumentos combinatórios), talvez.
-
alexandre32100
-
 por alexandre32100 » Qua Nov 24, 2010 13:06
por alexandre32100 » Qua Nov 24, 2010 13:06
Ah, um argumento seria o seguinte:

corresponde à contagem de quantos grupos de

elementos podemos formar a partir de um conjunto de

. Esta mesma contagem pode ser feita escolhendo quais os

elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),

grupos.
Assim conclui-se que
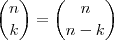
.
-
alexandre32100
-
 por victoreis1 » Qua Nov 24, 2010 20:12
por victoreis1 » Qua Nov 24, 2010 20:12
alexandre32100 escreveu:Ah, um argumento seria o seguinte:

corresponde à contagem de quantos grupos de

elementos podemos formar a partir de um conjunto de

. Esta mesma contagem pode ser feita escolhendo quais os

elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),

grupos.
Assim conclui-se que
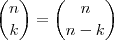
.
exatamente, pois para cada subconjunto

de elementos de

, haverá sempre um subconjunto complementar

, daí que há a mesma quantidade destes subconjuntos..
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Desafios Fáceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
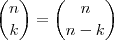 todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?

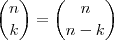 todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
 corresponde à contagem de quantos grupos de
corresponde à contagem de quantos grupos de  elementos podemos formar a partir de um conjunto de
elementos podemos formar a partir de um conjunto de  . Esta mesma contagem pode ser feita escolhendo quais os
. Esta mesma contagem pode ser feita escolhendo quais os  elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),
elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),  grupos.
grupos.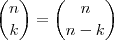 .
.corresponde à contagem de quantos grupos de
elementos podemos formar a partir de um conjunto de
. Esta mesma contagem pode ser feita escolhendo quais os
elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),
grupos.
.
 de elementos de
de elementos de  , haverá sempre um subconjunto complementar
, haverá sempre um subconjunto complementar  , daí que há a mesma quantidade destes subconjuntos..
, daí que há a mesma quantidade destes subconjuntos..