Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por victoreis1 » Qua Out 20, 2010 14:59
por victoreis1 » Qua Out 20, 2010 14:59
Boa tarde.. há dois anos, faço a OBM, e me deparo com questões muito desafiadoras, como esta:
PROBLEMA 5
Prove que o número
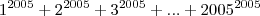
é múltiplo de

.
Queria saber como é feita, e também, se possível, uma introdução sobre congruência modular e divisibilidade, já que sou do primeiro ano e nunca tive contato com tais assuntos..
obrigado! ^^
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Qua Out 20, 2010 22:27
por VtinxD » Qua Out 20, 2010 22:27
Cara....poderia até tentar resolver por congruência(estou com uma ideia na cabeça

) mas você disse que ainda não sabe.Então acho que seria melhor se te disse-se um bom lugar para procurar material.
O site da OBMEP(OBM da escola publica) tem tudo que você pode até precisar para a terceira fase,se você chegar la tem que procurar uma igreja e se benze

.Segue o link:
http://www.obmep.org.br/prog_ic_2008/apostila2008.htmlCaso chegue na terceira fase e saiba inglês procure no site da IMO por materiais, são muito bons e complexos.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por victoreis1 » Qua Out 20, 2010 23:51
por victoreis1 » Qua Out 20, 2010 23:51
valeu pelo link, muito bons os pdfs de lá.. vo dar uma lida amanhã..
se vc souber como resolver, e tiver vontade, resolve a questão usando congruência modular e tal, que talvez dê pra entender..
valeu!
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Qui Out 21, 2010 20:40
por VtinxD » Qui Out 21, 2010 20:40
Espero que esteja certo :
Primeiro vamos analisar o 1+2+3+4+5+....+2005, que é uma PA de razão 1.Sua soma é dada por

Agora nós temos que provar que esse numero é divisivel por 2005 e por 1003:
Agora vou começar a usar a congruencia modular:

o que quer dizer que 2005 sempre deixa resto zero quando divido por 2005;

,uma propriedade da aritmética modular é:"O resto de uma soma e soma dos restos".Repetindo o processo anterior e somando os restos chegamos ao resto igual zero que representa que a soma é divisível pelo módulo.Provando que é divisível.
Agora só usar o mesmo método para 1003 ,provando que a soma também é disivel por 1003.E como 1003 e 2005 não possuem fatores comuns podemos inferir que a soma é disivel por 1+2+3...+2005.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por victoreis1 » Qui Out 21, 2010 20:53
por victoreis1 » Qui Out 21, 2010 20:53
VtinxD escreveu:Espero que esteja certo :
Primeiro vamos analisar o 1+2+3+4+5+....+2005, que é uma PA de razão 1.Sua soma é dada por

Agora nós temos que provar que esse numero é divisivel por 2005 e por 1003:
Agora vou começar a usar a congruencia modular:

o que quer dizer que 2005 sempre deixa resto zero quando divido por 2005;

,uma propriedade da aritmética modular é:"O resto de uma soma e soma dos restos".Repetindo o processo anterior e somando os restos chegamos ao resto igual zero que representa que a soma é divisível pelo módulo.Provando que é divisível.
Agora só usar o mesmo método para 1003 ,provando que a soma também é disivel por 1003.E como 1003 e 2005 não possuem fatores comuns podemos inferir que a soma é disivel por 1+2+3...+2005.
somando os restos teríamos
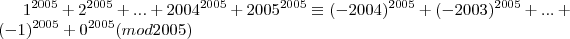
porque então chegamos ao resto zero?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Qui Out 21, 2010 21:49
por VtinxD » Qui Out 21, 2010 21:49
Foi mal...esqueci de falar:
só usar essa técnica até o numero 1002 no caso,pois ai os alternos se anulam.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisibilidade
por VtinxD » Qua Fev 09, 2011 02:11
- 1 Respostas
- 1513 Exibições
- Última mensagem por Renato_RJ

Qua Fev 16, 2011 00:13
Álgebra Elementar
-
- Divisibilidade
por igorcamilo » Sex Jun 24, 2011 19:20
- 1 Respostas
- 1201 Exibições
- Última mensagem por FilipeCaceres

Sex Jun 24, 2011 19:40
Álgebra Elementar
-
- [DIVISIBILIDADE]
por juliohenriquelima14 » Sáb Dez 13, 2014 23:20
- 1 Respostas
- 1457 Exibições
- Última mensagem por adauto martins

Dom Dez 21, 2014 11:49
Aritmética
-
- Divisibilidade
por Lucio » Sáb Fev 25, 2017 10:41
- 1 Respostas
- 1983 Exibições
- Última mensagem por petras

Qua Mar 08, 2017 19:30
Aritmética
-
- Divisibilidade, congruência
por ckde » Seg Ago 02, 2010 10:42
- 0 Respostas
- 1195 Exibições
- Última mensagem por ckde

Seg Ago 02, 2010 10:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
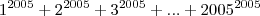 é múltiplo de
é múltiplo de  .
.
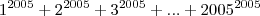 é múltiplo de
é múltiplo de  .
.
 ) mas você disse que ainda não sabe.Então acho que seria melhor se te disse-se um bom lugar para procurar material.
) mas você disse que ainda não sabe.Então acho que seria melhor se te disse-se um bom lugar para procurar material. .Segue o link:
.Segue o link:


 o que quer dizer que 2005 sempre deixa resto zero quando divido por 2005;
o que quer dizer que 2005 sempre deixa resto zero quando divido por 2005; ,uma propriedade da aritmética modular é:"O resto de uma soma e soma dos restos".Repetindo o processo anterior e somando os restos chegamos ao resto igual zero que representa que a soma é divisível pelo módulo.Provando que é divisível.
,uma propriedade da aritmética modular é:"O resto de uma soma e soma dos restos".Repetindo o processo anterior e somando os restos chegamos ao resto igual zero que representa que a soma é divisível pelo módulo.Provando que é divisível.
o que quer dizer que 2005 sempre deixa resto zero quando divido por 2005;
,uma propriedade da aritmética modular é:"O resto de uma soma e soma dos restos".Repetindo o processo anterior e somando os restos chegamos ao resto igual zero que representa que a soma é divisível pelo módulo.Provando que é divisível.
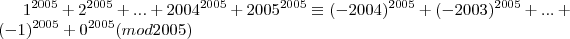


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
