Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por FcoEwerton » Qua Dez 15, 2010 16:03
por FcoEwerton » Qua Dez 15, 2010 16:03
Agora há uma distribuição de dinheiro. A primeira pessoa dá 3 qian, a seguinte 4 qian, a próxima pessoa 5 qian, e cada pessoa que se sucede dá mais 1 qian (do que a anterior). Depois da distribuição, juntam o dinheiro de todas e distribuem-no equitativamente. Cada pessoa recebe 100 qian. Descobre o número de pessoas.
-
FcoEwerton
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Dez 14, 2010 22:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por VtinxD » Qua Dez 15, 2010 19:04
por VtinxD » Qua Dez 15, 2010 19:04
Uma das soluções que encontrei foi essa:
Primeiro vamos descobrir qual total de dinheiro.Como é uma P.A a sequencia de cada dinheiro dado para cada pessoa podemos usar a fórmula de soma de P.A para achar o total:
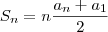
.Para destribuir equivalentemente basta dividir por n que teremos quanto cada um ganhou.
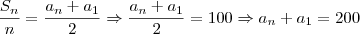
.Como

,valor que a primeira pessoa ganhou,

.
Espero estar certo.Valeu pelo desafio.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por FcoEwerton » Qua Dez 15, 2010 23:18
por FcoEwerton » Qua Dez 15, 2010 23:18
Está Correto, Parabéns!!!
-
FcoEwerton
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Dez 14, 2010 22:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aproximações de valores em dinheiro
por Lucas Ribeiro » Seg Set 24, 2012 12:15
- 0 Respostas
- 725 Exibições
- Última mensagem por Lucas Ribeiro

Seg Set 24, 2012 12:15
Matemática Financeira
-
- [Números naturais] Problema envolvendo dinheiro
por Georges123 » Sáb Fev 16, 2013 00:20
- 2 Respostas
- 1718 Exibições
- Última mensagem por Georges123

Dom Fev 17, 2013 17:09
Teoria dos Números
-
- distribuição de Poisson.
por saseong » Seg Dez 01, 2008 20:10
- 5 Respostas
- 10224 Exibições
- Última mensagem por Sandra Piedade

Dom Dez 28, 2008 17:19
Estatística
-
- Distribuição Binomial
por fono12345 » Qua Set 08, 2010 22:17
- 1 Respostas
- 5023 Exibições
- Última mensagem por Neperiano

Qua Set 14, 2011 19:49
Estatística
-
- Distribuição normal
por lanahwinchester » Qui Jun 30, 2011 13:58
- 2 Respostas
- 5891 Exibições
- Última mensagem por sena

Sáb Jul 30, 2011 12:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



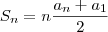 .Para destribuir equivalentemente basta dividir por n que teremos quanto cada um ganhou.
.Para destribuir equivalentemente basta dividir por n que teremos quanto cada um ganhou.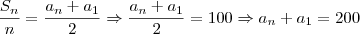 .Como
.Como  ,valor que a primeira pessoa ganhou,
,valor que a primeira pessoa ganhou, .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

