por joaofonseca » Qua Mar 21, 2012 13:28
por joaofonseca » Qua Mar 21, 2012 13:28
Seja um dado não equilibrado, com as faces numeradas de 1 a 6.Sabe-se que todos os números pares tem a mesma probabilidade da sair e que todos os numeros impares também têm a mesma probabilidade de sair.Sabe-se ainda que a probabilidade de sair número primo é de 0,4.
Qual é a probabilidade de sair 1?
Sejam dois acontecimentos:
A-"sair número impar"
B-"sair número primo"
Neste problema não se pode utilizar a regra de Laplace, pois os acontecimentos elementares não são equiprováveis.Contudo, no espaço amostral desta experiência, sair número primo implica sair número impar e vice-versa.Logo deduzi que a P(A) também é igual a 0,4.
É dito que os números impares tem a mesma probabilidade de sair.Ou seja o 1, o 3 e 5.
Logo cada um dos números impares tem

de 0,4 de probabilidade de sair.

Contudo a solução do livro é
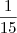
.Quem está errado?
Obrigado pela ajuda
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Sex Mar 23, 2012 18:19
por joaofonseca » Sex Mar 23, 2012 18:19
Após alguma pesquisa na net.Encontrei uma solução para o problema.
Primeiro o erro do meu racíocino anterior:
O nº 1 não é número primo, mas o 2 é.Logo existem 3 números pares (dos quais um deles é primo) e 3 números impares(dos quais 2 são primos).
Pela axiomática sabemos que a
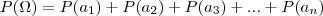
. em que

representa o universo e
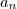
os vários acontecimentos que compõem o universo.
Existem 3 acontecimentos que têm a mesma probabilidade(nºs impares) e outros 3 acontecimentos também com a mesma probabilidade(nºs pares).Assim:

, em que
a é a probabilidade de ser par e
b a probabilidade de ser impar.
Sabemos que a probabilidade de ser nº primo é de 0,4.Logo:
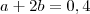
Agora basta montar um sistema, resolve-lo e achar o valor de
b para saber a probabilidade de sair o 1 (impar).
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificil questao de probabilidade
por bmachado » Seg Jun 11, 2012 16:29
- 2 Respostas
- 3572 Exibições
- Última mensagem por bmachado

Qua Jun 13, 2012 22:03
Probabilidade
-
- que dificil
por giboia90 » Seg Abr 08, 2013 03:34
- 1 Respostas
- 1465 Exibições
- Última mensagem por anabatista

Ter Abr 09, 2013 01:37
Estatística
-
- Primitiva difícil
por photon » Sáb Set 19, 2009 18:39
- 0 Respostas
- 1446 Exibições
- Última mensagem por photon

Sáb Set 19, 2009 18:39
Cálculo: Limites, Derivadas e Integrais
-
- questão dificil.
por natanskt » Seg Dez 13, 2010 18:20
- 1 Respostas
- 2443 Exibições
- Última mensagem por Molina

Sáb Dez 25, 2010 20:28
Binômio de Newton
-
- Viagem difícil
por Mechanic » Sex Mar 18, 2011 21:00
- 4 Respostas
- 2771 Exibições
- Última mensagem por MarceloFantini

Qua Mar 23, 2011 00:30
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 de 0,4 de probabilidade de sair.
de 0,4 de probabilidade de sair.
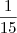 .Quem está errado?
.Quem está errado?

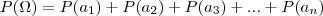 . em que
. em que  representa o universo e
representa o universo e 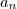 os vários acontecimentos que compõem o universo.
os vários acontecimentos que compõem o universo. , em que
, em que