 por Shirley » Seg Ago 10, 2015 22:58
por Shirley » Seg Ago 10, 2015 22:58
Um serviço deve ser realizado por indivíduos com a mesma capacidade de trabalho e trabalhando independentemente um dos outros. Nessas condições, três indivíduos realizaram 40% do serviço em 30 horas de trabalho. A esta altura, se acrescentarmos dois novos indivíduos nas mesmas condições, em quantas horas o serviço estará terminado?
A) 18
B) 24
C) 27
D) 100/1
E) 75
* Eu tentei resolver da seguinte forma:
indivíduos horas %
3 30 40
5 (corresponde a acrescentar mais 2 indivíduos) X 40

-
Shirley
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Ago 10, 2015 21:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Ter Ago 11, 2015 11:55
por nakagumahissao » Ter Ago 11, 2015 11:55
Shirley,
Esta questão é uma Regra de Três onde estão envolvidos proporões INVERSAMENTE proporcionais (Aumenta-se Homens e diminui-se as horas de realização deste mesmo trabalho), ou seja (Preste atenção nas flechinhas):
3 Homens ? = 40% do Serviço = 12 Horas ?
5 Homens ? = 40% do Serviço = x Horas ?
Assim, calculando as devidas proporções, temos:
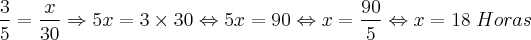

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Shirley » Ter Ago 11, 2015 12:08
por Shirley » Ter Ago 11, 2015 12:08
Muito obrigada pela ajuda
-
Shirley
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Ago 10, 2015 21:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema...me ajude a resolver por favor...
por Leandrin » Sáb Out 09, 2010 22:47
- 1 Respostas
- 2795 Exibições
- Última mensagem por Neperiano

Dom Out 10, 2010 11:57
Estatística
-
- regra de três
por DanielFerreira » Ter Set 22, 2009 14:17
- 3 Respostas
- 3705 Exibições
- Última mensagem por DanielFerreira

Qui Set 24, 2009 21:34
Álgebra Elementar
-
- Regra de três
por Daniel Gurgel » Qua Set 23, 2009 12:16
- 1 Respostas
- 2704 Exibições
- Última mensagem por Lucio Carvalho

Qui Set 24, 2009 03:51
Álgebra Elementar
-
- regra de tres
por aspirantestudante » Ter Jun 08, 2010 20:41
- 8 Respostas
- 9522 Exibições
- Última mensagem por DanielFerreira

Sex Set 10, 2010 20:45
Desafios Enviados
-
- Regra de três
por Mandu » Qua Out 20, 2010 16:19
- 3 Respostas
- 3515 Exibições
- Última mensagem por Mandu

Qui Out 21, 2010 22:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




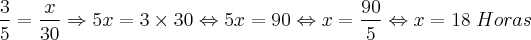





 , avisa que eu resolvo.
, avisa que eu resolvo.

