Primeiro de tudo, não sei se esse é o local certo para postar, peço desculpas se não for. Mas é uma dúvida que tnho, sobre um desafio que envolva probabilidade, então achei que aqui seria o local correto.
Eu e um conhecido estamos discutindo sobre a solução de um problema de matemática.
Que pode ser encontrado aqui, na questão 16, junto com um link para a resolução.
http://mathproblems.info/group1.html
A questão é a seguinte:
A box contains two coins. One coin is heads on both sides and the other is heads on one side and tails on the other. One coin is selected from the box at random and the face of one side is observed. If the face is heads what is the probability that the other side is heads?.
Uma tradução próxima seria essa:
Dentro de uma caixa há duas moedas. Uma moeda tem duas faces com "Cara" e a outra possui uma face "Cara" e outra "Coroa". Uma moeda é pega aleatoriamente e é observada sua face. Se a face observada for cara, qual é a probabilidade da outra face da moeda também ser cara?
Bom, eu pensei que já que temos uma face que é revelada e determinada pelo problema, é como se jogássemos a moeda e o resultado desse cara. Logo, a chance de ser cara, na outra face, é a mesma da chance de tirar uma moeda com dupla face cara. Ou seja, 50%
Daqui para frente, usarei:
C = Cara
Co = Coroa
Porém, meu conhecido insiste na solução vista em: http://mathproblems.info/prob16s.htm
Apresenta o seguinte pensamento:
Probabilidades das moedas:
Moeda/~~/ Face vista/~~/Face Oculta
Duas caras/~~/C¹/~~/C²
Duas caras/~~/C²/~~/C¹
Normal/~~/C/~~/Co
Normal/~~/Co/~~/C
Voltando o ao que o enigma diz, se a face for cara, qual a chance de a outra face tbm ser. O dono do site disse que é 2/3, tendo em vista a tabela acima, já que 3 dos resultados deram cara na face de cima e 2 deles tem a face de baixo como cara. Tem lógica, mas...
Aí que reside o problema:
A pergunta não foi "Se pegarmos aleatoriamente uma moeda e lançarmos qual a probabilidade de dar cara e a outra face também ser cara". Ai sim, talvez, esse resultado fosse satisfatório.
Mas a pergunta se refere a um resulta já obtido, como se fosse um lançamento já feito, e não à probabilidade de lançar a atingir resultados.
A questão diz que vimos uma face e que era Cara, ou seja, partimos da idéia que já temos um resultado. Logo, se a moeda de duas caras cair c¹/c² ou cair c²/c¹ não faz diferença. A pergunta é a respeito da probabilidade da face DE BAIXO ser cara.
O que vocês acham? Por favor postem cálculos e resolução se possível.


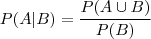
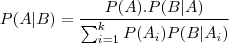
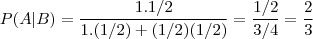




 , avisa que eu resolvo.
, avisa que eu resolvo.

