Bem, vamos escrever o espaço amostral
S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2.3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
Bem, só se tem uma chance de tirar 5 no primeiro lançamento e 3 no segundo lançamento como se pode observar.
Sendo
A=número tirado no primeiro dado
B=número tirado no segundo dado
O Teorema que você deveria usar é o da probabilidade total(ou teorema de Bayes) visto que se quer saber é a probabilidade de de se tirar 3 tal no segundo dado tal que se tirou 5 no primeiro.
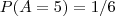
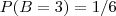
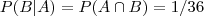
.
Se fosse ou, teríamos que verificar a probabilidade de se tirar 5 no primeiro ou a probabilidade de se tirar 3 no segundo de forma separada.
Desta forma:
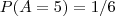
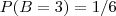
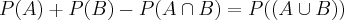
que dá o resultado que você falou

11/36
Nota: O lançamento de dados normalmente é independente, não há indicações no problema para considerarmos dependências aleatórias.


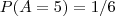
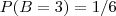
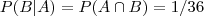 .
.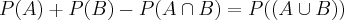
 11/36
11/36



 , avisa que eu resolvo.
, avisa que eu resolvo.

