 por tatimamedes » Sex Mar 01, 2013 20:40
por tatimamedes » Sex Mar 01, 2013 20:40
Pessoal, tudo bem com vocês?
Tenho um exercício para resolver, espero que vocês possam me ajudar.
É o seguinte:
Certo tipo de motor pode apresentar dois tipos de falhas: mancais presos e queima do induzido. Sabendo-se que as probabilidades de ocorrência dos defeitos são 0,2 e 0,03, respectivamente, determinar a probabilidade de que num motor daquele tipo, selecionado ao acaso, não ocorra, simultaneamente, as duas falhas.
A. 6%
B. 19,4%
C. 99,4%
D. 21,8%
E. 77,6%
Justifique sua resposta:
Resposta:
P(mp)=0,2*10=2
P(qi)=0,03*100=3
Eu já tentei de tudo. Fiz 0,2*0,03=0,006*100=0,6%
Também tentei dividir um pelo outro mas nada funcionou.
Por favor, me ajudem!!!
Obrigada
-
tatimamedes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 01, 2013 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
 por Rafael16 » Sex Mar 01, 2013 21:22
por Rafael16 » Sex Mar 01, 2013 21:22
Boa noite tatimamedes!
Se somarmos a probabilidade de ocorrer, simultaneamente, as duas falhas com a probabilidade de não ocorrer as duas falhas, isso dará 100%, ou 1. Concorda?
Por exemplo, a probabilidade de sair o número 2 em um dado é de 1/6 , logo a probabilidade de não sair o número 2 é de 5/6. Então, se somarmos as duas probabilidades vai dar 1.
Voltando ao problema...
x --> probabilidade de não ocorrer as duas falhas simultaneamente.
(0,2 * 0,03) + x = 1
x = 0,944
x = 94,4%
Letra "C"
Abraço!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por sauloandrade » Sex Mar 01, 2013 22:17
por sauloandrade » Sex Mar 01, 2013 22:17
Não sei se a reposta correta é letra C. Veja aqui a minha resolução:
A probabilidade de falhar os mancais presos é 0,2 logo a probabilidade de dar certo é
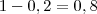
A probabilidade de falhar a queima do induzido é 0,03 logo a probabilidade de não falhar é
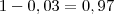
0,6
Então como você quer os dois simultaneamente, teremos

%
Você tem o gabarito?
-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por tatimamedes » Sex Mar 01, 2013 23:01
por tatimamedes » Sex Mar 01, 2013 23:01
Tenho sim. A resposta correta é a C.
-
tatimamedes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 01, 2013 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
 por tatimamedes » Sex Mar 01, 2013 23:04
por tatimamedes » Sex Mar 01, 2013 23:04
Pessoal, obrigada pela ajuda.
Tenho outro exercício. É o seguinte:
Suponhamos que existam, num certo mercado, duas fábricas de lâmpadas. A fábrica "A" produz 500 lâmpadas, das quais 25% apresentam defeitos e a fábrica "B" produz 550 lâmpadas, das quais 26% são defeituosas; vamos supor também que as 1050 lâmpadas são vendidas por um único vendedor. Por fim suponhamos que um cliente vai comprar uma lâmpada sem especificar marca e que estas foram dispostas ao acaso na prateleira. Calcular:
I - A probabilidade de se receber uma lâmpada defeituosa.
II - A probabilidade de, tendo se recebido uma lâmpada perfeita, ela ser da marca "B".
A alternativa que apresenta as respostas corretas é a:
A - I = 47,62% e II = 26,00%,
B - I = 26,00% e II = 52,05%,
C - I = 25,52% e II = 26,00%,
D - I = 25,50% e II = 50,00%,
E - I = 25,52% e II = 52,05%.
Justifique sua resposta:
Eu já tentei de tudo sem sucesso. Eis a minha resolução:
Resposta:
Fábrica Produção % de peças defeituosas
A 500 25%
B 550 26%
Total 1050 106%
a) P[peça defeituosa] =
P[peça defeituosa fabricada em A] + P[peça defeituosa fabricada em B] =
Probabilidade [peça fabricada em A E peça defeituosa] +
Probabilidade [peça fabricada em B E peça defeituosa] =
500*0,25 + 550*0,26= 125+143=268 268*100=26800
b) P(B/boa) =??
Por favor, me ajudem a resolver e a entender onde estou errando. Muito obrigada.
-
tatimamedes
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 01, 2013 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração de Empresas
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10336 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21644 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5341 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4516 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4530 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



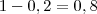
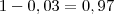
 %
%