qual a probabilidade

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

qual a probabilidade

Regras do fórum
Responder

qual a probabilidade

Mensagempor Ana Maria da Silva » Sex Abr 11, 2014 00:20

preciso ver o desenvolvimento Urgente!

Em caixa com doze peças três delas são defeituosas. São selecionadas duas peças ao acaso sem reposição .
a) Obtenha a probabilidade de nenhuma peça ser defeituosa
b) Obtenha a probabilidade de pelo menos uma ser defeituosa
Ana Maria da Silva
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 83
Registrado em: Qua Mar 27, 2013 15:09
Formação Escolar: ENSINO MÉDIO
Área/Curso: licenciatura em matemática
Andamento: cursando
Voltar ao topo

Re: qual a probabilidade

Mensagempor fff » Sex Abr 11, 2014 15:17

Boa tarde. Encontrei um exercício muito parecido com esse:https://br.answers.yahoo.com/question/index?qid=20080717051512AA1A1fl
Esta é a minha resolução (não tenho a certeza se está certo):
a)
\frac{9}{12}*\frac{8}{11}=\frac{72}{132}=\frac{6}{11}

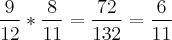
b)p(uma ser defeituosa e outra não)+p(uma não ser defeituosa e outra ser)+p(duas serem defeituosas)
\frac{3}{12}*\frac{9}{11}*2+\frac{3}{12}*\frac{2}{11}=\frac{5}{11}
Avatar do usuário
fff
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 103
Registrado em: Sáb Dez 21, 2013 11:30
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Informática
Andamento: cursando
Voltar ao topo
Responder

Voltar para Probabilidade

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

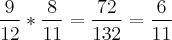
Índice do fórum