Boa tarde galera, tudo bem? Estou estudando probabilidade para concursos públicos e me deparei com essas duas questões, gostaria de saber como monto a resolução delas ... A do primeiro exercício até encontrei a resolução, é 13/14, mas não sei como monto e a segunda me deixou todo confuso !
Segue abaixo:
1 - Uma equipe de socorro, formada por 4 médicos, deve ser escolhida, aleatoriamente, dentre 4 cirurgiões e 6 ortopedistas. Qual é a probabilidade de que o grupo escolhido tenha pelo menos um cirurgião?
2 - Numa sala estão 10 homens e 6 mulheres. Dos 10 homens, 4 usam óculos e das 6 mulheres, 4 não usam óculos. Escolhendo-se ao acaso uma pessoa dessa sala, determine a probabilidade de que a pessoa escolhida seja um homem ou alguém sem óculos.
Ps.: Alguém me recomenda uma apostila ou material explicativo que mostre passo-a-passo a realizar resoluções desse tipo?
Desde de já agradeço !
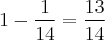. Como são poucas possibilidades é possível que se monte um árvore de probabilidades para facilitar a visualização.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)