 por LadyTrilleras » Sex Out 11, 2013 16:46
por LadyTrilleras » Sex Out 11, 2013 16:46
Numa sorveteria são oferecidos 5 sabores de cobertura e 4 tipos de granulado. De quantas maneiras é possível cobrir um sorvete utilizando-se duas coberturas e pelo menos 2 tipos de granulados?
Eu estava resolvendo assim:
coberturas granulados
--- x --- x --- x ---
5 4 2 2
20 x 4
80 formas de cobrir o sorvete,
porém a resposta é 110
Eu não consegui entender nada do que o livro disse, me ajudem por favor.
segundo o livro: Resolução:
2 coberturas: C5,2 = 10
Pelo menos 2 tipos de granulado:
C4,2 = 6
C4,3 = 4
C4,4 = 1
Total de maneiras:
10 . (C4,2+ C4,3+ C4,4) = 10 . (6+4+1) = 10 . 11 = 110
Fonte: DANTE, Luiz Roberto. Matemática. Volume Único. 1ª ed. São Paulo: Editora Ática, 2008.
-
LadyTrilleras
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Out 11, 2013 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Saúde
- Andamento: cursando
 por Luis Gustavo » Sex Out 11, 2013 17:16
por Luis Gustavo » Sex Out 11, 2013 17:16
Você pode escolher as duas coberturas de
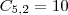
maneiras.
O granulado dá um pouco mais de trabalho de calcular: podemos escolher dois, três ou quatro tipos de granulado.
Dois tipos de granulados
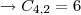
maneiras.
Três tipos de granulados
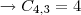
maneiras.
Quatro tipos de granulados

maneiras.
Daí, o total de maneiras é

.
Entendeu?
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LadyTrilleras » Sex Out 11, 2013 18:00
por LadyTrilleras » Sex Out 11, 2013 18:00
Clareou um pouco, desculpa gente ... eu tenho muita dificuldade com matemática. Obrigada!
-
LadyTrilleras
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Out 11, 2013 16:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Saúde
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Amigos estou com dificuldades em resolver esse problema
por Catriane Moreira » Sáb Nov 20, 2010 22:54
- 1 Respostas
- 1598 Exibições
- Última mensagem por esteban

Sáb Nov 27, 2010 22:09
Matemática Financeira
-
- [Probabilidade Condicionada] Dificuldades
 por N0namePT » Sáb Mai 24, 2014 15:44
por N0namePT » Sáb Mai 24, 2014 15:44
- 1 Respostas
- 3202 Exibições
- Última mensagem por Diofanto

Dom Set 14, 2014 23:05
Probabilidade
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3703 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- Compreender Resultado de Inequação
por johnlaw » Dom Mar 20, 2011 17:53
- 4 Respostas
- 2969 Exibições
- Última mensagem por Dan

Dom Mar 20, 2011 20:07
Sistemas de Equações
-
- Ajuda para resolver!!
por Optikool » Dom Dez 02, 2012 21:31
- 2 Respostas
- 3202 Exibições
- Última mensagem por Optikool

Ter Dez 04, 2012 22:22
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


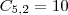 maneiras.
maneiras. 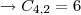 maneiras.
maneiras.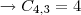 maneiras.
maneiras. maneiras.
maneiras. .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.