Determine a probabilidade de ser escolhido um vestido, sabendo que foi previamente seleccionada a fábrica A.
|Vestidos | Casacos |
-------------------------------------
Fábrica A | 240 | 540 |
Fábrica B | 460 | 220 |
-------------------------------------
PS: Desculpem a qualidade da tabela



 . Destas, a quantidade fabricada por A é
. Destas, a quantidade fabricada por A é  . Portanto,
. Portanto, 
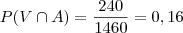

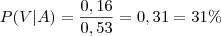



 , avisa que eu resolvo.
, avisa que eu resolvo.

