Lança-se um dado cubico, perfeito, numerado de 1 a 6, até obter o número 6.Qual a probabilidade de ter de lançar o dado pelo menos duas vezes para obter o númeo 6 uma vez?
Este exercicio partiu-me a cabeça toda! Pois, foge aos processos/técnicas normais à resolução de problemas de probabilidades.Até que fui ver a solução.Mas a solução não explicava o raciocinio.Então tive novamente de puxar pela cabeça para ver como chegar lá. A solução é 5/6.
Então pensei.
é a probabilidade do acontecimento contrário ao acontecimento de probabilidade 
.No meio do texto introdutório tive de encontrar qual era o acontecimento para o qual era pedido a probabilidade.
Seja A o acontecimento " lançar o dado pelo menos duas vezes".
será "lançar o dado exatamente uma vez".Ora a probabilidade de é pois cada face do dado tem igual probabilidade de sair.Logo está explicado o raciocinio por de trás do resultado. Sabem de outra forma para resolver este problema?
.
.
.
por 
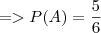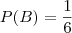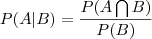
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.