Seja um dado não equilibrado, com as faces numeradas de 1 a 6.Sabe-se que todos os números pares tem a mesma probabilidade da sair e que todos os numeros impares também têm a mesma probabilidade de sair.Sabe-se ainda que a probabilidade de sair número primo é de 0,4.
Qual é a probabilidade de sair 1?
Sejam dois acontecimentos:
A-"sair número impar"
B-"sair número primo"
Neste problema não se pode utilizar a regra de Laplace, pois os acontecimentos elementares não são equiprováveis.Contudo, no espaço amostral desta experiência, sair número primo implica sair número impar e vice-versa.Logo deduzi que a P(A) também é igual a 0,4.
É dito que os números impares tem a mesma probabilidade de sair.Ou seja o 1, o 3 e 5.
Logo cada um dos números impares tem
 de 0,4 de probabilidade de sair.
de 0,4 de probabilidade de sair.
Contudo a solução do livro é
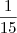 .Quem está errado?
.Quem está errado?Obrigado pela ajuda


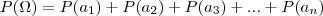 . em que
. em que  representa o universo e
representa o universo e 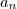 os vários acontecimentos que compõem o universo.
os vários acontecimentos que compõem o universo. , em que
, em que 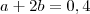


 :
: