Em um projeto de visita a escolas do batalhão, estão envolvidos três sargentos e dez soldados. Para uma visita, é formado um grupo com um sargento e três soldados; porém, devido às atividades do quartel, os soldados Araújo e Batista não poderão estar no mesmo grupo. Dessa forma, determine de quantas maneiras distintas pode-se formar esse grupo.
A) 24
B) 32
C) 132
D) 216
O que eu tentei:
(1)
Primeiro, fiz a combinação sem considerar a regra (Araújo e Batista no mesmo grupo), encontrando o máximo de combinações possíveis:
Entre os soldados:
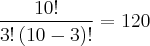
Segundo passo: calculei o número de combinações em que Araújo e Batista ficariam no mesmo grupo:
Entre os soldados:
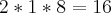
Considerando apenas os soldados, a diferença entre o total de possibilidades e as possibilidades em que ambos os soldados estão no mesmo grupo resulta em:

Considerando a combinação entre os sargentos e soldados:

(2)
Considerei que Araújo e Batista fossem uma única pessoa:
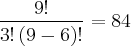
Considerando a combinação entre os sargentos e soldados:
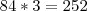
-
Tendo em vista os resultados, ambos não estão entre as alternativas. Se alguém puder esclarecer esta questão, ficarei grato.


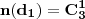 ;
;
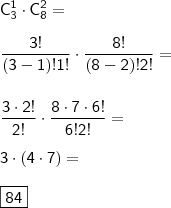
 .
. 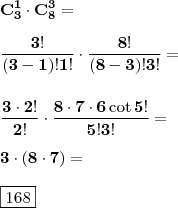


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
