Quantas são as soluções inteiras positivas de
 ?
?Minha solução:
Como queremos soluções inteiras positivas, então as variáveis devem receber valores inteiros estritamente maiores do que zero. Logo, devem ser maiores ou iguais a 1. Assim, por exemplo, x ? 1 => x – 1 ? 0. Portanto, a inequação dada pode ser substituída por: a + b + c < 7, onde a = x – 1, b = y – 1, c = z – 1 são variáveis não-negativas. Como ainda é uma desigualdade, basta colocarmos uma variável de folga f. Assim, a + b + c + f = 7. Agora, podemos seguir a mesma ideia do esquema de "traço-bola". Vamos permutar 3 “traços” e 7 “bolas”. Logo, temos (10!)/((3!)(7!)) = 120 soluções.
A resposta certa é 84.
Por que a minha solução está errada? Onde errei?
Muito Obrigada!





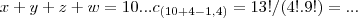
 ,demonstrarei tal fato mais a frente...em nosso caso,errei o dados,logo:
,demonstrarei tal fato mais a frente...em nosso caso,errei o dados,logo: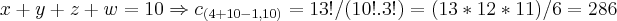
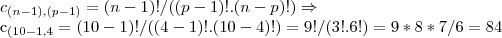

 .
.
 :
: