Bom, eu não estou conseguindo entender por que estou errando na solução.
Fiz assim:
O primeiro grupo pode ser escolhido de
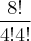 modos. E o segundo
modos. E o segundo  . Ok. Aí, multiplicando eu encontro 70. Mas esta não é resposta. Por que raios a resposta é 35? Já me disseram que ''você contou a divisão duas vezes'' mas como assim? Já pensei pensei e pensei mas eu não consigo entender... muito grato a quem puder dar uma luz nesta questão.
. Ok. Aí, multiplicando eu encontro 70. Mas esta não é resposta. Por que raios a resposta é 35? Já me disseram que ''você contou a divisão duas vezes'' mas como assim? Já pensei pensei e pensei mas eu não consigo entender... muito grato a quem puder dar uma luz nesta questão.






 .
.
 :
: