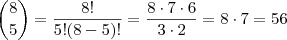Análise Combinatória

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Análise Combinatória

Regras do fórum
Responder

Análise Combinatória

Mensagempor thamysoares » Sex Jul 19, 2013 19:46

UFRJ - Uma pessoa possui 5 livros de física e 7 livros de matemática. De quantos modos distintos ela pode distribuir estes livros em uma estante de modo que dois ou mais livros de física nunca fiquem juntos?

Eu pensei em fazer assim:
M.F.M.F.M.F.M.F.M.F.M.M
7.5.6.4.5.3.4.2.3.1.2.1
Mas dá um número enorme e a RESPOSTA que está na minha apostila É: 56 :s

Me ajudem?
thamysoares
Usuário Ativo
Usuário Ativo
 
Mensagens: 23
Registrado em: Qua Nov 14, 2012 19:21
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: Análise Combinatória

Mensagempor MateusL » Sex Jul 19, 2013 22:58

Pela resposta que está na apostila, deves considerar todos os livros de matemática idênticos, bem como todos os livros de física.

Primeiramente, coloque os 7 livros de matemática na estante, o que poderá ser feito de apenas um modo, pois todos os livros de matemática são idênticos. Agora terás 8 "vagas" para os livros de física: no início, entre o primeiro e o segundo livro de matemática, entre o segundo e o terceiro,..., entre o sexto e o sétimo ou no fim.

Como são cinco livros de física, deverás escolher cinco dentre as oito vagas disponíveis, o que dará:

{8\choose 5}=\dfrac{8!}{5!(8-5)!}=\dfrac{8\cdot 7\cdot 6}{3\cdot 2}=8\cdot 7=56

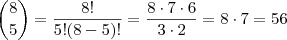
Abraço!
MateusL
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 68
Registrado em: Qua Jul 17, 2013 23:25
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica
Andamento: cursando
Voltar ao topo
Responder

Voltar para Análise Combinatória

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum