Boa Tarde.
Gostaria de ajuda para essa questão, por favor. Não consigo chegar no resultado.
Um baralho é composto por 52 cartas, sendo 13 de cada naipe. Os naipes são: copas, ouros, espadas e paus; e as cartas, para cada naipe são: A (as),2,3...,10, J(valete),Q (dama) e K(rei). As cartas de um baralho comum foram distribuídas em duas caixas da seguinte maneira: Na caixa X, foram colocadas todas as cartas de ouros e de paus e na caixa Y, todas as cartas de espada e de copas. Deseja-se retirar, ao acaso, sucessivamente e sem reposição , 3 cartas da caixa X e, em seguida 2 cartas da caixa Y.
a) Em quantas sequencias distintas aparecem os 4 ases e 1 rei? R.: 24
b) Em quantas sequencias distintas aparecem os 4 ases? R.: 288


 podemos pegar qquer carta das 52 disponiveis,teremos a seguite configuraçao:
podemos pegar qquer carta das 52 disponiveis,teremos a seguite configuraçao:
 pode ser qualquer q. nao seja As...pelo principio da multiplicaçao teremos:
pode ser qualquer q. nao seja As...pelo principio da multiplicaçao teremos:
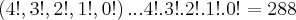

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)