Olá
Russman! Pensei no seguinte:
Inicialmente, devemos encontrar o menor e o maior... São eles: 1023 e 6397.
Avaliemos as possibilidades... MILHAR.
(i) fixando o 1º algarismo e o último temos:
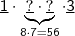
Mas, note que o último dígito poderá ser o 5, o 7 e o 9. Desse modo,
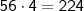
.
(ii) fixando o 1º algarismo em 2, teremos:
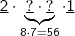
Mas, teremos também 3, 5, 7 e 9. Portanto,
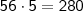
.
(iii) fixando o 3 na unidade de milhar, a quantidade de números será calculada de maneira análoga à (i). Com efeito, teremos 224 números.
(iv) fixando o 4 na unidade de milhar, a quantidade de números será calculada de modo análogo ao item (ii), ou seja, 280.
(v) fixando o 5 na unidade de milhar... 224.
(vi) fixando o 6, devemos ficar atento ao máximo... Sendo assim, devemos esmiuçar as possibilidades. Segue,
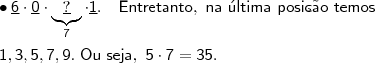

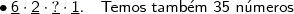
Por fim, avaliamos
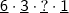
. Que, é o mesmo que
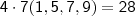
.
Logo, temos que:
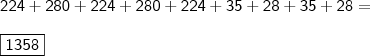
Tens o gabarito?
Até!


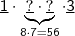
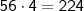 .
.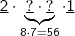
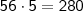 .
.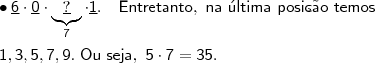

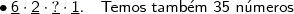
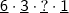 . Que, é o mesmo que
. Que, é o mesmo que 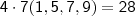 .
.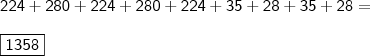



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.